算法设计与分析

前言

算法设计与分析实验还挺有趣，简单记录一下，以后可能还能用上

贪心算法应用(求图的最小生成树)

实验过程(请用简单的文字描述)

1. 算法核心

   prime算法，根据顶点，每次找到一个最小边然后进行标记，按照已有的点，继续搜索

   kruskal算法，按照权值从小到大的顺序选择n-1条边，并保证这n-1条边不构成回路

2. 造数据，n∈[100,1000]且 n%20==0 的顶点，随机生成任意顶 点之间的权值，并输出其邻接矩阵，通过计时功能绘制 n 与求解时间的曲线图， 关键点就是在原有算法的基础之上加入随机数，计时功能以及使用邻接矩阵存图 而非邻接表

3. 实验过程大计划 使用c++进行编写，excel做可视化数据分析

实验详细操作步骤或程序清单

1. 造数据

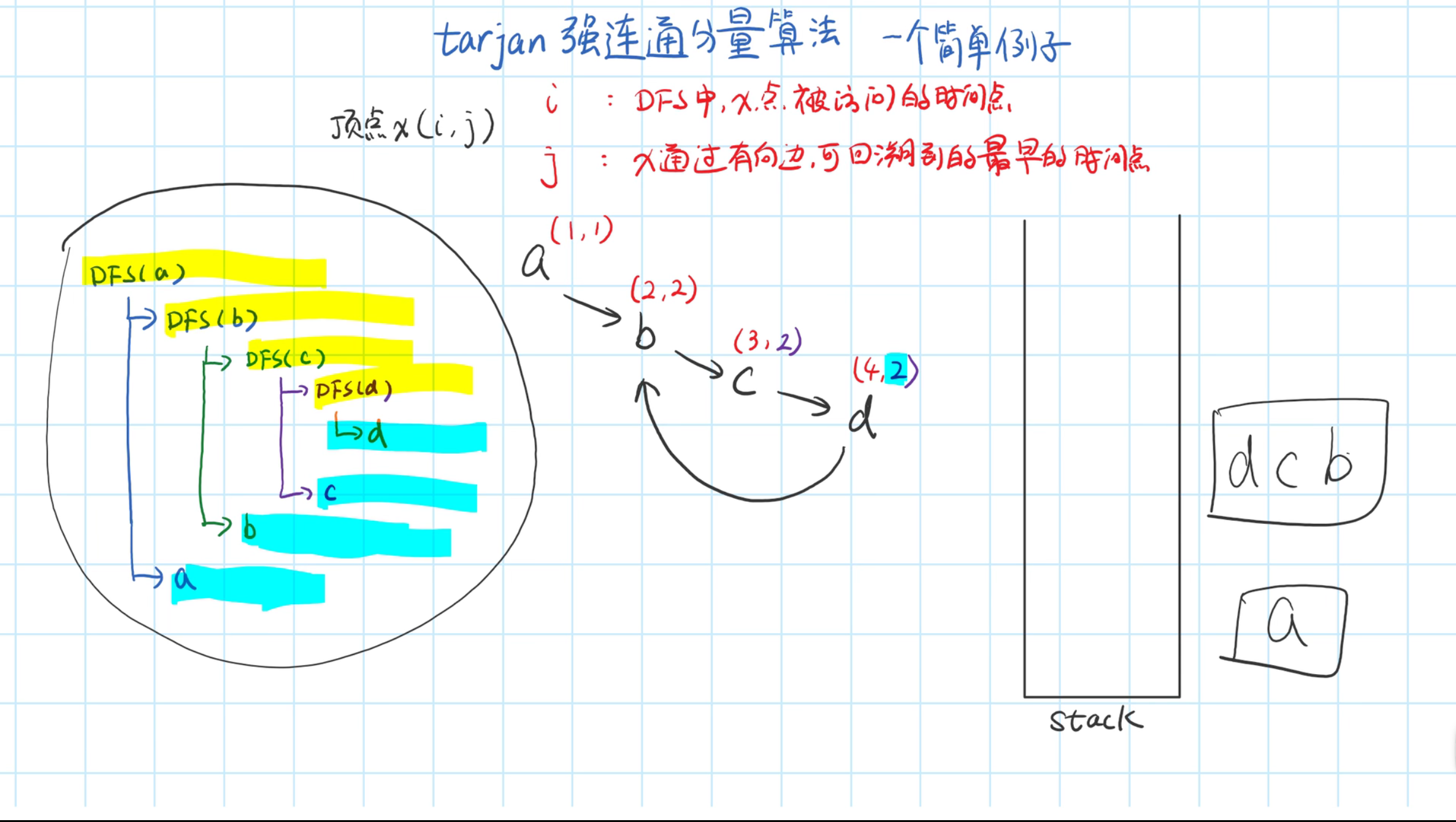
   对于随机造出的图，要满足是强连通图才能有最小生成树，所以要先判断什么时候生成了强连通图，采用Tarjan算法，借助堆栈数据结构，进行是否是强连通图的判断

   Tarjan算法核心思想:

2. 算法实现

   使用prim kruskal算法实现最小生成树算法，在实现的过程中加入

time函数实现对程序运行时间的计算

3. 数据可视化

   使用excel对生成的数据进行折线图，可视化

4. 程序清单

   //判断是否是强连通图 Tarjan算法
   void Tarjan(int u, int pre) {
       int v;
       LOW[u] = DFN[u] = ++Index;
       Stack[top++] = u;
       Instack[u] = true;
       int pre_cnt = 0;
       for (int i = head[u]; i != -1; i = edge[i].next) {
           v = edge[i].to;
           if (v == pre && pre_cnt == 0) {
               pre_cnt++;
               continue;
           }
           if (!DFN[v]) {
               Tarjan(v, u);
               if (LOW[u] > LOW[v]) LOW[u] = LOW[v];
               if (LOW[v] > DFN[u]) {
                   bridge++;
                   putss[number++] = edge[i].w;
                   edge[i].cut = true;
                   edge[i ^ 1].cut = true;
               }
           } else if (Instack[v] && LOW[u] > DFN[v])
               LOW[u] = DFN[v];
       }
       if (LOW[u] == DFN[u]) {   // 如果low和dfn相等说明为强连通图，出栈
           scc++;
           do {
               v = Stack[--top];
               Instack[v] = false;
               Belong[v] = scc;
               num[scc]++;
           } while (v != u);
       }
   }

   // prime算法
   int prim(int cost[][maxn], int n) {
       int ans = 0;
       memset(vis, 0, sizeof(vis));
       vis[1] = true;
       for (int i = 2; i <= n; ++i) {
           lowc[i] = cost[1][i];
       }
       for (int i = 2; i <= n; ++i) {
           int minc = inf;
           int p = -1;
           for (int j = 1; j <= n; ++j) {
               if (!vis[j] && minc > lowc[j]) {
                   minc = lowc[j];
                   p = j;
               }
           }
           if (minc == inf) return -1;
           ans += minc;         //最小生成树长度
           vis[p] = true;       //找到最短的边访问
           for (int j = 1; j <= n; ++j) {
               if (!vis[j] && lowc[j] > cost[p][j]) {
                   lowc[j] = cost[p][j];
               }
           }
       }
       return ans;  // 树的最小权值
   }

   //Kruskal算法
   int Kruskal(int n) {
       memset(F, -1, sizeof(F));
       sort(edgee, edgee + tol, cmp);
       int cnt = 0;
       int ans = 0;
       for (int i = 0; i < tol; ++i) {
           int u = edgee[i].u;
           int v = edgee[i].v;
           int w = edgee[i].w;
           int t1 = Find(u);
           int t2 = Find(v);
           if (t1 != t2) {
               ans += w;
               F[t1] = t2;
               cnt++;
           }
           if (cnt == n - 1) break;
       }
       if (cnt < n - 1) return -1;
       else return ans;
   }

程序总代码清单

Kruskal算法

   #include
   #include

Kruskal算法

   #include
   #include

实验结果

prim算法

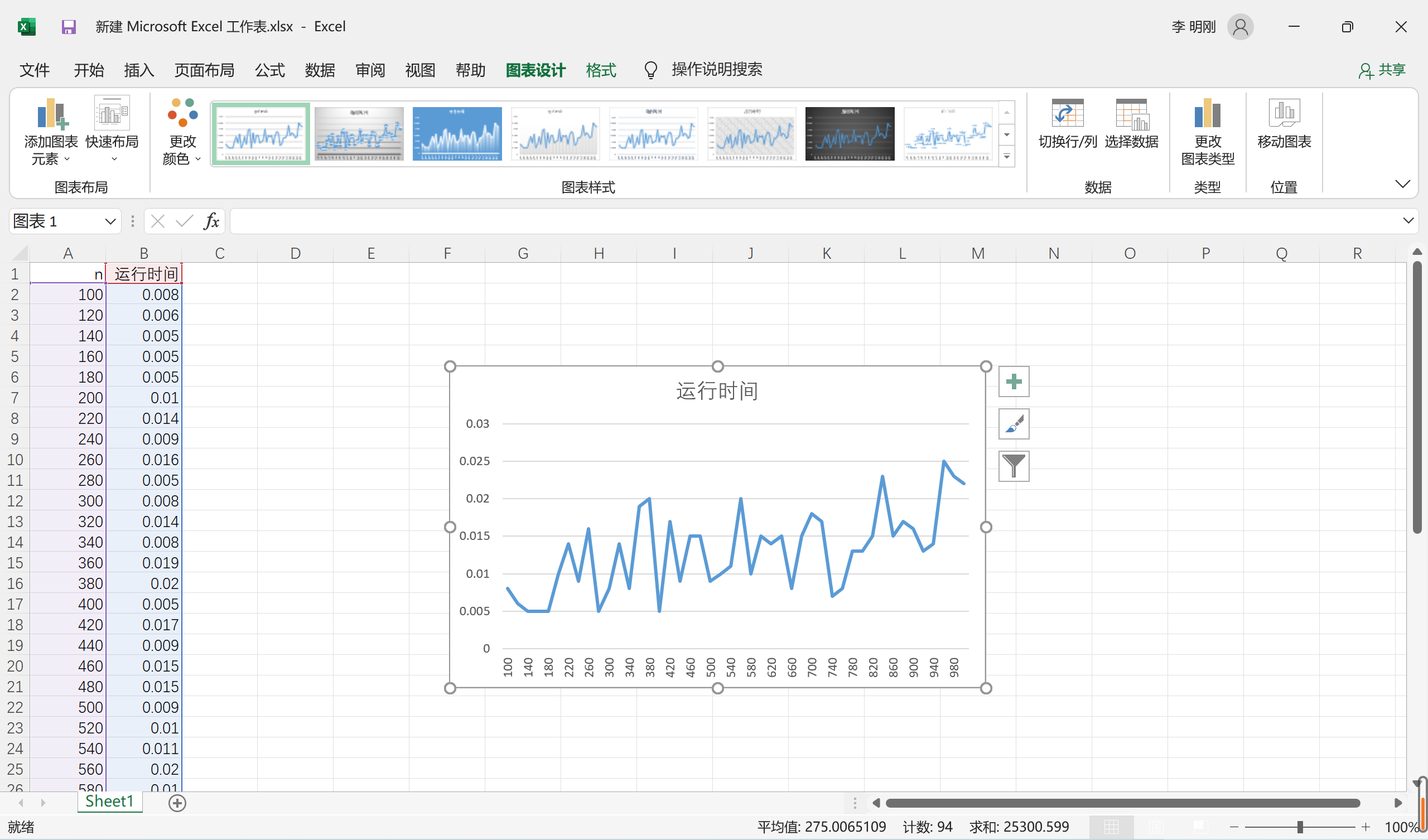
n    运行时间
100    0.008
120    0.006
140    0.005
160    0.005
180    0.005
200    0.01
220    0.014
240    0.009
260    0.016
280    0.005
300    0.008
320    0.014
340    0.008
360    0.019
380    0.02
400    0.005
420    0.017
440    0.009
460    0.015
480    0.015
500    0.009
520    0.01
540    0.011
560    0.02
580    0.01
600    0.015
620    0.014
640    0.015
660    0.008
680    0.015
700    0.018
720    0.017
740    0.007
760    0.008
780    0.013
800    0.013
820    0.015
840    0.023
860    0.015
880    0.017
900    0.016
920    0.013
940    0.014
960    0.025
980    0.023
10000.022

数据可视化

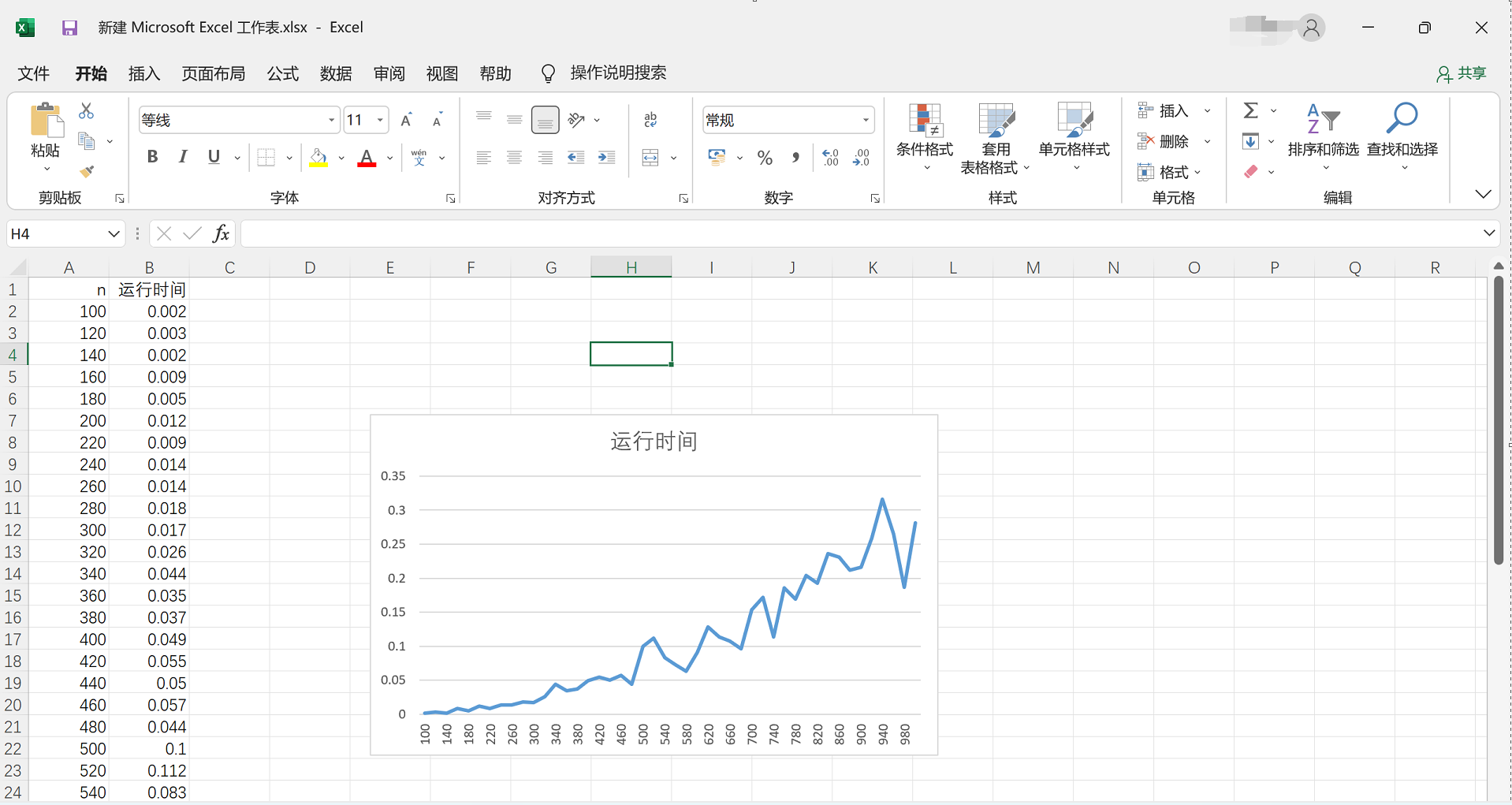
kruska算法

n	运行时间
100	0.002
120	0.003
140	0.002
160	0.009
180	0.005
200	0.012
220	0.009
240	0.014
260	0.014
280	0.018
300	0.017
320	0.026
340	0.044
360	0.035
380	0.037
400	0.049
420	0.055
440	0.05
460	0.057
480	0.044
500	0.1
520	0.112
540	0.083
560	0.073
580	0.063
600	0.091
620	0.128
640	0.114
660	0.108
680	0.096
700	0.154
720	0.172
740	0.114
760	0.186
780	0.169
800	0.204
820	0.193
840	0.236
860	0.231
880	0.212
900	0.216
920	0.259
940	0.316
960	0.265
980	0.187
1000	0.281

实验环境

excel

c++

CLion

疑难小结

1. 学会了通过运行时间来看时间复杂度，更具有可观性

2. 学会了如何造数据，使用随机产生数据，加边

3. 本次实验还是有缺陷，对于n个节点，但是边的个数还是随机的，对时间复杂度是有影响的，造成产生的数据不太理想

4. 由于程序运行过快，有时无法计算时间，所以采用sleep函数，相当于将函数上移动，来更好的展示运算时间，并不影响实验结果

   分治算法应用(分治法进行快速排序)

   1.实验过程(请用简单的文字描述)

5. 分治法的核心思想:

   对于一个规模为n的问题

• 若该问题可以很容易地解决则直接解决
• 否则将其分解为k个规模较小地子问题，子问题互为相互独立且与原问题形式相同，递归地解这些子问题，然后将各个子问题地解合并到原来问题。

2. 使用随机数构建数据
3. 使用逆序对，观察无序度与求解用时之间的关系，采用树状数组降低逆序对的时间复杂度
4. 实验计划: 使用golang进行编写

实验详细操作步骤或程序清单

1. 造数据

   使用rand()随机数生成[0:3000]随机数

2. 数据可视化

   使用excel快速生成线性图

3. 程序清单

   • 分治法实现快排

     func quicksort(mapp []int, start int, end int) {
         if start >= end {
             return
         }
         mid := mapp[end]
         left := start
         right := end - 1
         for left < right {
             for mapp[left] <= mid && left < right {
                 left++
             }
             for mapp[right] >= mid && left < right {
                 right--
             }
             mapp[left], mapp[right] = mapp[right], mapp[left]
         }
         if mapp[left] >= mapp[end] {
             mapp[left], mapp[end] = mapp[end], mapp[left]
         } else {
             left++
         }
         quicksort(mapp, start, left-1)
         quicksort(mapp, left+1, end)
     }

   • 基于树状数组逆序度计算

     func RandInt(min, max int) int { //生成随机数
         if min >= max || min == 0 || max == 0 {
             return max
         }
         return rand.Intn(max-min) + min
     }
     func add(number int) { //构造树状数组
         for number <= n {
             a[number]++
             number += number & (-number)
         }
     }
     func sum(number int) int {
         var ros = 0
         for number > 0 {
             ros += a[number]
             number -= number & (-number)
         }
         return ros
     }

   4.总代码

   package main
   
   import (
       "fmt"
       "math/rand"
       "time"
   )
   
   const maxm = 1e6 + 100
   
   type edge struct {
       v, indexX int
   }
   type outdate struct {
       num      int
       since    int
       ReNumber int
   }
   
   var (
       a    []int
       n    int
       mapp []int
   )
   
   func RandInt(min, max int) int { //生成随机数
       if min >= max || min == 0 || max == 0 {
           return max
       }
       return rand.Intn(max-min) + min
   }
   func add(number int) { //构造树状数组
       for number <= n {
           a[number]++
           number += number & (-number)
       }
   }
   func sum(number int) int {
       var ros = 0
       for number > 0 {
           ros += a[number]
           number -= number & (-number)
       }
       return ros
   }
   func quicksort(mapp []int, start int, end int) {
       if start >= end {
           return
       }
       mid := mapp[end]
       left := start
       right := end - 1
       for left < right {
           for mapp[left] <= mid && left < right {
               left++
           }
           for mapp[right] >= mid && left < right {
               right--
           }
           mapp[left], mapp[right] = mapp[right], mapp[left]
       }
       if mapp[left] >= mapp[end] {
           mapp[left], mapp[end] = mapp[end], mapp[left]
       } else {
           left++
       }
       quicksort(mapp, start, left-1)
       quicksort(mapp, left+1, end)
   }
   func main() {
       outDate := make(map[int]outdate)
       var ran = 1
       for n = 5000; n < 70000; n++ {
           if n%1000 != 0 {
               continue
           }
           a = make([]int, maxm)     //初始化a
           mapp = make([]int, maxm)  //初始化mapp
           num := make(map[int]edge) //初始化num
           for i := 1; i <= n; i++ {
               mapp[i] = RandInt(1, 3000)
               num[i] = edge{mapp[i], i}
           }
           var ans int
           for i := 1; i <= n; i++ {
               add(num[i].v)
               ans += i - sum(num[i].v)
           }
           timeStart := time.Now()
           time.Sleep(1)
           quicksort(mapp, 1, n)
           time := time.Since(timeStart)
           var lnng int
           lnng = int(time)
           outDate[ran] = outdate{n, lnng, ans}
           ran++
       }
       fmt.Println("n", "\t", "运行时间", "\t", "逆序数")
       for i := 1; i <= len(outDate); i++ {
           fmt.Println(outDate[i].num, "\t", outDate[i].since, "\t", outDate[i].ReNumber)
       }
   }

   实验结果

   程序运行结果

n 运行时间 逆序数 关系

n      运行时间      逆序数
5000      1994200      6356121
6000      1995100      9040812
7000      1995000      12396920
8000      1007400      16006480
9000      1007100      20515333
10000      1007200      24850212
11000      1035900      30253245
12000      2003100      35732922
13000      2061800      42291037
14000      2036400      49252042
15000      1074600      56332533
16000      1995100      64094125
17000      1960800      71984640
18000      2991700      81453485
19000      2992000      90144560
20000      2991900      99901035
21000      1995400      110389537
22000      1994800      121226617
23000      1994900      132573949
24000      1960600      143831396
25000      1994600      157058071
26000      2991600      169758526
27000      1994700      181467202
28000      1994800      195298608
29000      2990700      208739750
30000      2961700      224304156
31000      2991900      239514881
32000      3024000      256139437
33000      2993100      273357833
34000      2991500      288262128
35000      3989400      303134819
36000      3972700      324349369
37000      2992400      341968957
38000      2992000      362811077
39000      3023000      379705268
40000      2991800      401399685
41000      3960900      418710348
42000      2991400      439585949
43000      2992700      459663399
44000      2991700      483275595
45000      4219700      505158612
46000      3989200      527494105
47000      4985200      551917130
48000      3989600      574285522
49000      3988700      602612851
50000      4986400      624353709
51000      5026700      650897222
52000      3987800      676202613
53000      4987400      702068237
54000      3988800      726560480
55000      4986000      754356142
56000      4986300      782166133
57000      4987200      812816980
58000      4985900      839324596
59000      5983200      873485002
60000      4985300      898002509
61000      4985100      931301443
62000      6944000      959866945
63000      4985100      992412366
64000      5020600      1027614728
65000      5019500      1058824736
66000      4986900      1084218111
67000      4984200      1120431731
68000      6950300      1155706503
69000      5014700      1191768434

进程 已完成，退出代码为 0

数据可视化

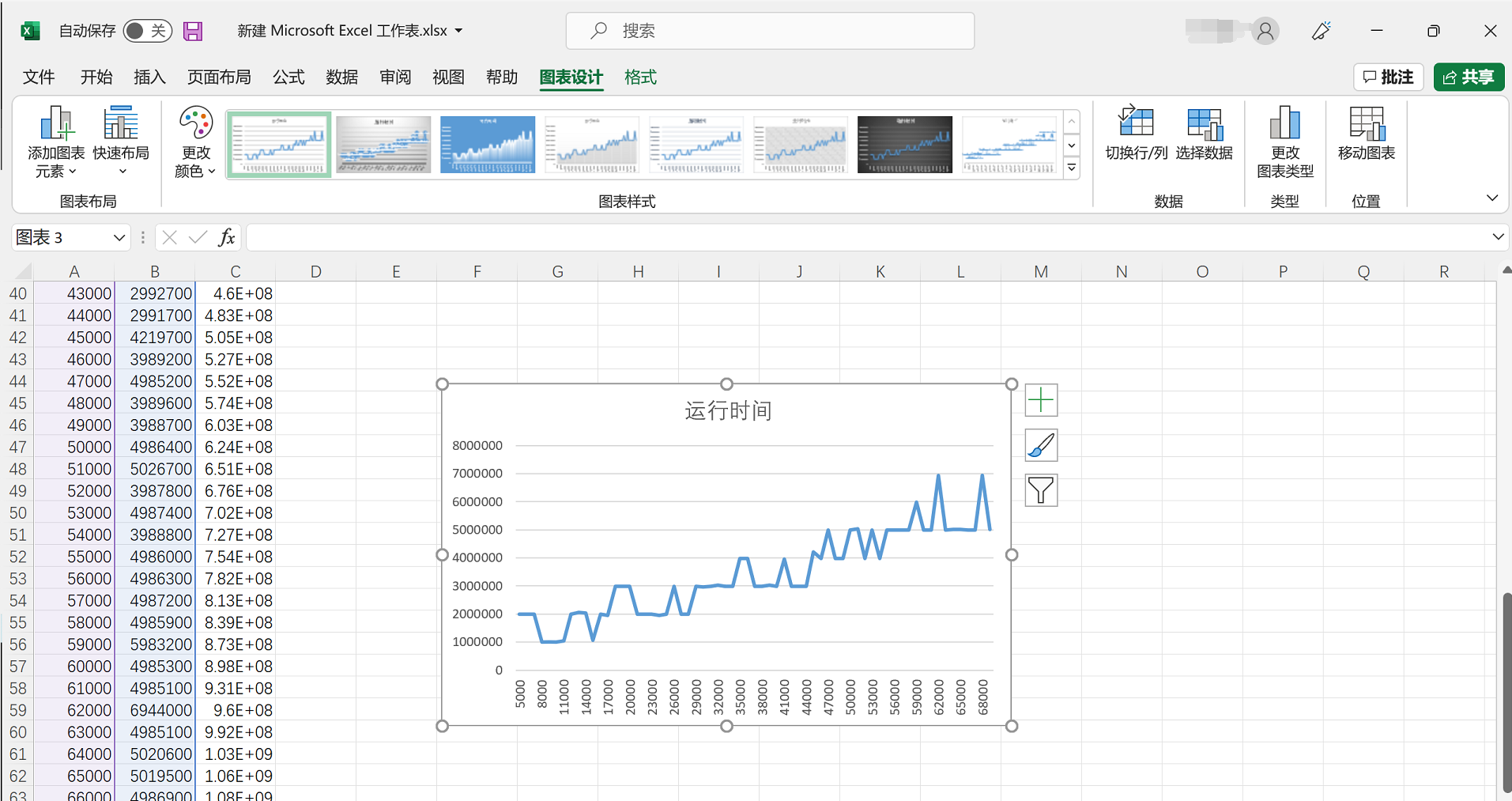
n与运算时间关系

无序度与运行时间关系

通过数据可视化可以发现，时间复杂段是O(n),跟实际的快排算法的时间复杂度相同

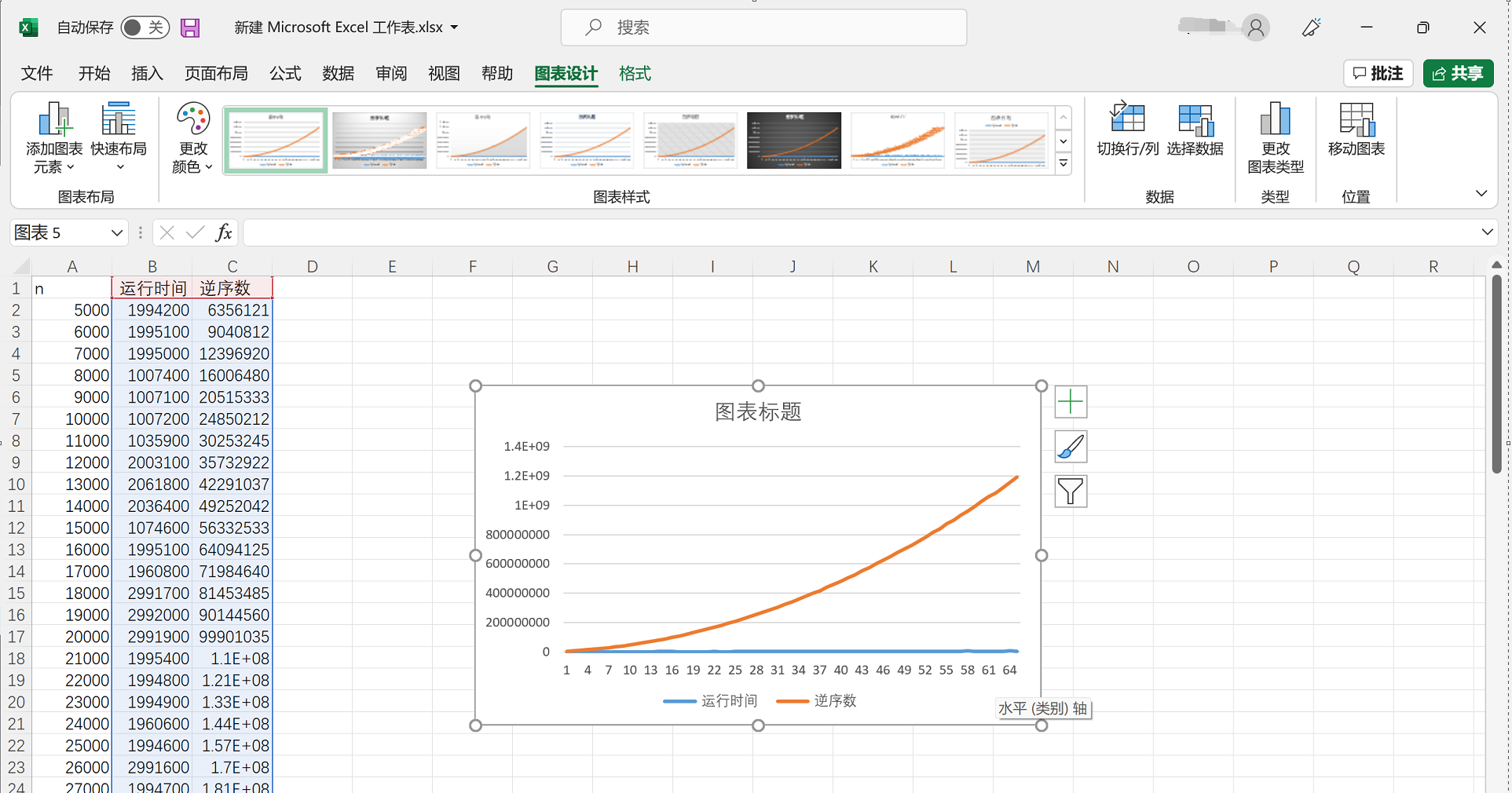
通过数据可视化可以发现 对于无序度和程序的运行时间来说 大致上也呈现出直线趋势

实验环境

goland

excel

疑难小结

1. 最开始的时候对于无序度的计算有点懵，后来通过资料查询发现只需要计算 逆序对的个数就行了，然后绘制成图

2. 以前对于时间复杂度的分析是通过计算类似 for 循环的层数计算的，没有通 过程序的运行时间确定过，通过本次实验从程序的运行时间的角度出发，我从更 详细的时间上面对这两种算法有了更加深刻的认识。

3. 随机数的生成还有待改进

   动态规划算法应用(求解编辑距离)

   实验过程(请用简单的文字描述)

4. 动态规划法的核心思想

   •最优子结构性质

   –原问题的最优解包含了其子问题的最优解，即原问题可以由子问题的最优解组合而成，这就使得问题可以拆分成若干个子问题。

   •子问题重叠性质

   –每次产生的子问题并不总是新问题，有些子问题被反复计算多次。

5. 使用随机长度的字符串构建数据

6. 使用m与n的之间的差来观察关系

7. 实验计划:使用golang进行编写

实验详细操作步骤或程序清单

1. 造数据

   使用rand()生成随机数字，在将数字转化为字符串

2. 数据可视化

   使用excel快速生成线性图

3. 程序清单

   • 动态规划法求解编辑距离

     func minDistance(word1 string, word2 string) {
         m := len(word1)
         n := len(word2)
         dp = make([][]int, m+1)
         for i := 0; i < m+1; i++ {
             dp[i] = make([]int, n+1)
         }
         for i := 0; i <= m; i++ { // 列初始化
             dp[i][0] = i
         }
         for i := 0; i <= n; i++ { // 行初始化
             dp[0][i] = i
         }
         for i := 0; i < m; i++ {
             for j := 0; j < n; j++ { // 横着填
                 if word1[i] == word2[j] { //如果第i个相等
                     dp[i+1][j+1] = dp[i][j]
                 } else {
                     dp[i+1][j+1] = Min(dp[i][j], Min(dp[i][j+1], dp[i+1][j])) + 1 //上方 右方 斜方 最小值 + 1
                 }
     
             }
         }
     }

   • 随机长度的字符串生成

     const char = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
     
     func RandomStr(len int) string {
         var str string
         for i := 0; i < len; i++ {
             random := rand.Int() % 26 //大写字母65-90
             strTemp := char[random]
             str = str + string(strTemp)
         }
         return str
     }

4. 总代码

   package main
   
   import (
       "fmt"
       "math/rand"
       "time"
   )
   
   var dp [][]int
   
   const char = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
   
   func RandomStr(len int) string {
       var str string
       for i := 0; i < len; i++ {
           random := rand.Int() % 26 //大写字母65-90
           strTemp := char[random]
           str = str + string(strTemp)
       }
       return str
   }
   func RandInt(min, max int) int { //生成随机数
       if min >= max || min == 0 || max == 0 {
           return max
       }
       return rand.Intn(max-min) + min
   }
   
   func main() {
       //var (
       //    S1 string
       //    S2 string
       //)
       //fmt.Printf("S1=")
       //fmt.Scanln(&S1)
       //fmt.Printf("S2=")
       //fmt.Scanln(&S2)
       //minDistance(S1, S2)
       fmt.Println("m\tn\tm*n\t求解用时")
       for i := 1000; i <= 3000; i++ {
           if i%10 != 0 {
               continue
           }
           str1Len := RandInt(i-500, i)
           str1 := RandomStr(str1Len)
           str2Len := RandInt(i, i+500)
           str2 := RandomStr(str2Len)
           startTime := time.Now()
           time.Sleep(1)
           minDistance(str1, str2)
           sinceTime := time.Since(startTime)
           fmt.Println(str1Len, "\t", str2Len, "\t", str1Len*str2Len, "\t", sinceTime)
       }
   }
   func Min(x, y int) int {
       if x <= y {
           return x
       }
       return y
   }
   
   func minDistance(word1 string, word2 string) {
       m := len(word1)
       n := len(word2)
       dp = make([][]int, m+1)
       for i := 0; i < m+1; i++ {
           dp[i] = make([]int, n+1)
       }
       for i := 0; i <= m; i++ { // 列初始化
           dp[i][0] = i
       }
       for i := 0; i <= n; i++ { // 行初始化
           dp[0][i] = i
       }
       for i := 0; i < m; i++ {
           for j := 0; j < n; j++ { // 横着填
               if word1[i] == word2[j] { //如果第i个相等
                   dp[i+1][j+1] = dp[i][j]
               } else {
                   dp[i+1][j+1] = Min(dp[i][j], Min(dp[i][j+1], dp[i+1][j])) + 1 //上方 右方 斜方 最小值 + 1
               }
   
           }
       }
   }
   
   //func solve(m int, n int) {
   //    if m == 0 || n == 0 {
   //        os.Exit(0)
   //    }
   //    if dp[m][n] == (dp[m-1][n] + 1) {
   //        fmt.Printf("S1第%d删除\n", m) // 上方
   //        solve(m-1, n)
   //    }
   //    if dp[m][n] == (dp[m][n-1] + 1) {
   //        fmt.Printf("S1第%d插入S2第%d位字母\n", m, n) //左侧
   //
   //        solve(m, n-1)
   //    }
   //    if dp[m][n] == dp[m-1][n-1] {
   //        //字符串相等什么也不用做
   //        solve(m-1, n-1)
   //    }
   //    if dp[m][n] == (dp[m-1][n-1] + 1) {
   //        //替换
   //        fmt.Printf("S1第%d替换为S2第%d位字母\n", m, n)
   //        solve(m-1, n-1)
   //    }
   //}

实验结果

程序运行结果

m与n的差距很小时

m	n	m*n	求解用时
991	993	984063	5.9836ms
1009	1000	1009000	4.9882ms
1015	1017	1032255	3.9915ms
1024	1024	1048576	4.9867ms
1038	1030	1069140	5.9849ms
1042	1040	1083680	4.0141ms
1051	1053	1106703	3.9647ms
1063	1064	1131032	3.9883ms
1072	1074	1151328	4.0261ms
1089	1081	1177209	4.9821ms
1095	1094	1197930	3.9911ms
1109	1107	1227663	4.953ms
1112	1112	1236544	3.9907ms
1124	1128	1267872	4.9856ms
1133	1139	1290487	4.9878ms
1141	1148	1309868	4.02ms
1150	1151	1323650	3.949ms
1161	1165	1352565	3.9538ms
1174	1171	1374754	4.9875ms
1185	1186	1405410	3.989ms
1193	1196	1426828	3.989ms
1201	1208	1450808	7.9625ms
1210	1214	1468940	5.9884ms
1226	1225	1501850	7.0111ms
1232	1239	1526448	5.9848ms
1246	1243	1548778	5.9737ms
1250	1253	1566250	4.999ms
1265	1262	1596430	4.9869ms
1276	1273	1624348	6.9824ms
1284	1289	1655076	6.9804ms
1299	1295	1682205	6.9829ms
1302	1301	1693902	5.9517ms
1312	1318	1729216	6.9807ms
1320	1324	1747680	4.9858ms
1331	1337	1779547	6.9828ms
1344	1345	1807680	5.984ms
1351	1354	1829254	5.9812ms
1366	1360	1857760	8.5188ms
1378	1378	1898884	6.9794ms
1385	1388	1922380	7.9879ms
1390	1397	1941830	6.9724ms
1404	1403	1969812	8.9748ms
1413	1416	2000808	8.0117ms
1427	1428	2037756	8.9748ms
1434	1434	2056356	6.9812ms
1446	1442	2085132	8.9976ms
1451	1457	2114107	8.9695ms
1461	1465	2140365	9.0067ms
1471	1477	2172667	10.9716ms
1482	1489	2206698	7.9463ms
1496	1492	2232032	8.014ms
1508	1500	2262000	7.9484ms
1517	1513	2295221	7.977ms
1522	1527	2324094	7.9784ms
1535	1530	2348550	9.0084ms
1546	1543	2385478	8.9439ms
1553	1555	2414915	9.9936ms
1566	1565	2450790	8.013ms
1575	1572	2475900	11.0009ms
1589	1587	2521743	8.9439ms
1595	1598	2548810	7.9773ms
1607	1604	2577628	8.9836ms
1611	1610	2593710	8.9728ms
1624	1626	2640624	11.0018ms
1634	1638	2676492	9.9754ms
1649	1640	2704360	8.9409ms
1654	1654	2735716	11.0007ms
1666	1668	2778888	11.9368ms
1679	1677	2815683	10.9791ms
1686	1680	2832480	9.9979ms
1693	1694	2867942	10.9407ms
1708	1704	2910432	11.9653ms
1713	1711	2930943	10.9746ms
1722	1721	2963562	9.9731ms
1733	1734	3005022	10.0068ms
1742	1743	3036306	9.9704ms
1751	1754	3071254	10.9764ms
1762	1763	3106406	9.9772ms
1777	1774	3152398	12.0012ms
1784	1781	3177304	10.9378ms
1796	1790	3214840	12.0007ms
1807	1800	3252600	14.9262ms
1810	1816	3286960	13.9607ms
1829	1827	3341583	19.9472ms
1838	1838	3378244	15.9591ms
1841	1849	3404009	16.9469ms
1857	1851	3437307	12.966ms
1864	1860	3467040	12.9634ms
1879	1877	3526883	11.9607ms
1883	1889	3556987	14.9607ms
1896	1893	3589128	12.9653ms
1902	1900	3613800	14.9925ms
1910	1917	3661470	13.9315ms
1927	1929	3717183	15.9907ms
1934	1935	3742290	14.957ms
1942	1941	3769422	15.9907ms
1953	1956	3820068	14.928ms
1960	1969	3859240	16.9545ms
1975	1970	3890750	13.994ms
1989	1984	3946176	16.9555ms
1991	1991	3964081	14.9637ms
2000	2009	4018000	15.9232ms
2019	2018	4074342	14.9946ms
2025	2028	4106700	15.9576ms
2033	2038	4143254	13.9947ms
2046	2043	4179978	14.9275ms
2057	2059	4235363	16.9872ms
2066	2065	4266290	17.9765ms
2075	2070	4295250	17.95ms
2084	2083	4340972	15.9883ms
2092	2092	4376464	18.9497ms
2103	2106	4428918	15.9484ms
2110	2118	4468980	17.9501ms
2120	2127	4509240	15.9526ms
2135	2138	4564630	15.956ms
2143	2142	4590306	15.9922ms
2159	2155	4652645	15.9917ms
2168	2165	4693720	16.9518ms
2176	2179	4741504	15.9887ms
2180	2185	4763300	16.9602ms
2199	2190	4815810	20.9522ms
2205	2200	4851000	17.9317ms
2219	2216	4917304	18.9519ms
2228	2225	4957300	16.9224ms
2235	2232	4988520	19.947ms
2241	2247	5035527	16.9559ms
2251	2259	5085009	17.953ms
2265	2261	5121165	18.9498ms
2278	2272	5175616	16.954ms
2282	2285	5214370	16.9544ms
2298	2298	5280804	20.9427ms
2308	2309	5329172	19.8551ms
2316	2313	5356908	19.9456ms
2327	2321	5400967	20.9445ms
2336	2335	5454560	21.9404ms
2349	2345	5508405	19.9447ms
2357	2355	5550735	18.9478ms
2362	2368	5593216	18.9479ms
2371	2374	5628754	18.951ms
2389	2380	5685820	18.9498ms
2392	2391	5719272	20.4511ms
2401	2402	5767202	21.9436ms
2418	2416	5841888	22.9362ms
2427	2421	5875767	24.9316ms
2433	2436	5926788	23.9375ms
2443	2443	5968249	24.916ms
2456	2457	6034392	22.9317ms
2461	2460	6054060	22.9386ms
2474	2473	6118202	21.9389ms
2487	2480	6167760	21.94ms
2490	2499	6222510	22.9383ms
2500	2504	6260000	22.9394ms
2511	2514	6312654	25.9297ms
2523	2522	6363006	21.9438ms
2535	2535	6426225	26.896ms
2546	2540	6466840	21.9792ms
2551	2556	6520356	21.9487ms
2561	2569	6579209	23.905ms
2570	2576	6620320	23.935ms
2585	2585	6682225	24.9638ms
2598	2590	6728820	23.9084ms
2603	2608	6788624	24.9604ms
2614	2617	6840838	24.8999ms
2622	2625	6882750	24.9339ms
2637	2635	6948495	22.8962ms
2646	2648	7006608	23.9356ms
2650	2657	7041050	22.9679ms
2666	2666	7107556	23.9658ms
2677	2674	7158298	24.9051ms
2685	2684	7206540	25.9515ms
2699	2696	7276504	26.9307ms
2700	2700	7290000	25.9568ms
2716	2710	7360360	27.9266ms
2729	2729	7447441	26.9244ms
2736	2735	7482960	27.9305ms
2745	2749	7546005	27.9218ms
2751	2754	7576254	31.9322ms
2761	2761	7623121	27.9239ms
2772	2771	7681212	31.8898ms
2784	2787	7759008	26.93ms
2793	2793	7800849	28.916ms
2802	2800	7845600	29.8895ms
2816	2819	7938304	28.9011ms
2826	2824	7980624	27.891ms
2830	2835	8023050	30.988ms
2846	2848	8105408	29.8887ms
2858	2856	8162448	31.9147ms
2864	2861	8193904	28.9223ms
2871	2874	8251254	27.9545ms
2884	2880	8305920	28.4225ms
2891	2898	8378118	31.9144ms
2906	2903	8436118	32.9117ms
2917	2910	8488470	29.4683ms
2927	2922	8552694	30.8867ms
2939	2938	8634782	29.9553ms
2944	2945	8670080	31.3555ms
2952	2959	8734968	29.8886ms
2969	2962	8794178	30.9186ms
2970	2970	8820900	31.9444ms
2981	2983	8892323	34.8759ms
2999	2995	8982005	31.949ms

m与n差距增大时候

m	n	m*n	求解用时
581	1283	745423	5.7179ms
865	1253	1083845	7.9796ms
903	1104	996912	5.9825ms
826	1447	1195222	6.9824ms
995	1296	1289520	7.979ms
666	1395	929070	6.0201ms
585	1497	875745	6.0188ms
683	1336	912488	5.0194ms
1016	1556	1580896	9.013ms
949	1288	1222312	8.9378ms
773	1487	1149451	6.9952ms
741	1179	873639	5.9552ms
694	1177	816838	4.0084ms
823	1608	1323384	6.9807ms
1015	1532	1554980	8.0138ms
1057	1272	1344504	6.9777ms
692	1338	925896	5.9524ms
1124	1545	1736580	9.0065ms
829	1430	1185470	6.9816ms
881	1513	1332953	8.2014ms
933	1353	1262349	7.0173ms
986	1464	1443504	8.0681ms
839	1362	1142718	6.9874ms
750	1258	943500	4.9549ms
1205	1644	1981020	10.0074ms
879	1325	1164675	5.2384ms
1160	1550	1798000	9.9417ms
1173	1616	1895568	10.0593ms
1074	1731	1859094	10.0038ms
862	1781	1535222	8.9775ms
1063	1397	1485011	8.2221ms
936	1520	1422720	8.9696ms
872	1804	1573088	7.9798ms
1137	1658	1885146	10.0572ms
907	1458	1322406	10.9944ms
1270	1466	1861820	11.0025ms
1315	1373	1805495	9.9491ms
1161	1519	1763559	16.9863ms
1302	1643	2139186	11.9381ms
1221	1474	1799754	9.0126ms
1037	1800	1866600	11.9298ms
1006	1648	1657888	8.9774ms
1227	1903	2334981	12.9631ms
1193	1754	2092522	11.004ms
1401	1754	2457354	12.1206ms
1386	1648	2284128	11.9376ms
989	1674	1655586	8.9756ms
1285	1476	1896660	10.9711ms
1397	1775	2479675	15.9572ms
1359	1583	2151297	13.9604ms
1389	1707	2371023	14.9599ms
1211	1765	2137415	13.9619ms
1027	1612	1655524	10.9739ms
1088	1983	2157504	14.0391ms
1480	1840	2723200	15.9875ms
1526	1976	3015376	16.9532ms
1338	2036	2724168	13.9963ms
1543	1686	2601498	12.9641ms
1430	2034	2908620	16.4305ms
1120	2087	2337440	11.968ms
1267	1784	2260328	10.0052ms
1118	1838	2054884	11.9673ms
1257	1993	2505201	12.1624ms
1587	1821	2889927	14.9934ms
1424	1681	2393744	14.1805ms
1390	1822	2532580	13.997ms
1197	1781	2131857	12.1608ms
1367	1676	2291092	12.9788ms
1458	1800	2624400	15.9887ms
1199	1859	2228941	10.9691ms
1639	1824	2989536	15.9873ms
1540	1900	2926000	16.9179ms
1353	2103	2845359	13.9611ms
1231	1968	2422608	13.0009ms
1628	2223	3619044	17.9514ms
1545	1899	2933955	14.9274ms
1320	2042	2695440	14.0809ms
1500	2109	3163500	16.9505ms
1490	1806	2690940	14.9595ms
1577	1833	2890641	15.0376ms
1629	2122	3456738	17.9528ms
1649	2064	3403536	16.9854ms
1400	2221	3109400	16.9864ms
1795	2289	4108755	19.9493ms
1725	1908	3291300	17.463ms
1813	2237	4055681	19.9774ms
1725	1954	3370650	16.9526ms
1764	1916	3379824	17.985ms
1489	1958	2915462	14.2071ms
1644	2302	3784488	19.9237ms
1592	1942	3091664	15.9559ms
1801	2035	3665035	18.1071ms
1574	2274	3579276	17.9812ms
1692	2163	3659796	17.9199ms
1644	2122	3488568	18.9504ms
1932	2091	4039812	18.976ms
1735	2090	3626150	17.9508ms
1882	2037	3833634	20.9768ms
1872	2297	4299984	21.9416ms
1768	2339	4135352	18.9808ms
1867	2183	4075661	23.9362ms
1894	2184	4136496	19.9759ms
1709	2421	4137489	22.9397ms
1828	2405	4396340	22.9243ms
1706	2233	3809498	20.9449ms
2035	2195	4466825	20.9772ms
1978	2354	4656212	23.9351ms
2012	2135	4295620	22.9384ms
1997	2082	4157754	20.9815ms
1638	2336	3826368	20.9807ms
1786	2210	3947060	20.1737ms
1769	2460	4351740	27.8925ms
1882	2248	4230736	24.932ms
1872	2393	4479696	22.9386ms
2046	2409	4928814	23.9359ms
1762	2527	4452574	21.9746ms
1695	2574	4362930	21.9427ms
1746	2233	3898818	19.9445ms
1685	2232	3760920	18.948ms
2144	2670	5724480	30.949ms
2045	2571	5257695	28.9498ms
2018	2583	5212494	27.4543ms
1903	2642	5027726	23.9207ms
2096	2241	4697136	23.2096ms
1986	2259	4486374	20.9175ms
1956	2315	4528140	23.9394ms
2182	2265	4942230	24.9266ms
2197	2602	5716594	29.8894ms
2258	2292	5175336	28.9211ms
1799	2315	4164685	21.9726ms
2261	2323	5252303	25.9026ms
2143	2632	5640376	27.4368ms
1966	2393	4704638	23.9367ms
1935	2517	4870395	24.9424ms
2302	2427	5586954	26.9276ms
1950	2723	5309850	28.9193ms
2289	2409	5514201	28.9534ms
2297	2402	5517394	26.9016ms
2211	2592	5730912	27.957ms
2256	2797	6310032	32.4114ms
2116	2814	5954424	27.9251ms
2349	2591	6086259	30.9188ms
2004	2763	5537052	27.1717ms
2007	2472	4961304	26.9281ms
1976	2645	5226520	28.929ms
1961	2819	5528059	28.3222ms
2147	2655	5700285	27.8957ms
2227	2738	6097526	30.9158ms
2364	2532	5985648	29.9213ms
2291	2722	6236102	32.9736ms
2268	2855	6475140	33.9105ms
2218	2662	5904316	32.8799ms
2376	2892	6871392	34.2158ms
2312	2599	6008888	29.9197ms
2194	2596	5695624	26.9297ms
2260	2628	5939280	32.5455ms
2249	2767	6222983	31.081ms
2201	3000	6603000	30.9186ms
2297	2605	5983685	30.0624ms
2210	2679	5920590	27.892ms
2412	2777	6698124	32.9409ms
2444	3003	7339332	35.1895ms
2141	3001	6425141	34.1741ms
2362	3045	7192290	35.9059ms
2362	3062	7232444	36.8917ms
2314	2683	6208462	30.9601ms
2440	2720	6636800	33.14ms
2347	2719	6381493	29.9195ms
2476	3141	7777116	38.8705ms
2584	2922	7550448	39.893ms
2517	2708	6816036	32.9386ms
2307	2909	6711063	34.9063ms
2258	3033	6848514	35.3544ms
2488	3110	7737680	38.8958ms
2686	3164	8498504	41.887ms
2374	2873	6820502	35.3624ms
2558	2940	7520520	38.0998ms
2731	3154	8613574	41.9011ms
2511	3068	7703748	36.9061ms
2743	3232	8865376	44.2455ms
2656	3004	7978624	38.9271ms
2337	3096	7235352	36.8674ms
2565	3133	8036145	41.4045ms
2663	3269	8705347	44.9085ms
2428	2905	7053340	33.91ms
2697	3294	8883918	41.996ms
2741	2957	8105137	41.8873ms
2848	3223	9179104	43.8556ms
2609	3188	8317492	38.9274ms
2451	3241	7943691	37.9006ms
2784	2922	8134848	38.897ms
2621	3206	8402926	40.891ms
2733	3023	8261859	39.8934ms
2440	3364	8208160	39.8619ms
2852	3129	8923908	43.1585ms
2735	3152	8620720	41.1268ms
2672	3322	8876384	41.8865ms
2966	3011	8930626	52.885ms
2797	3294	9213318	46.8428ms
2697	3039	8196183	39.921ms
2819	3068	8648692	40.8868ms

数据可视化

m*n与运行时间的关系

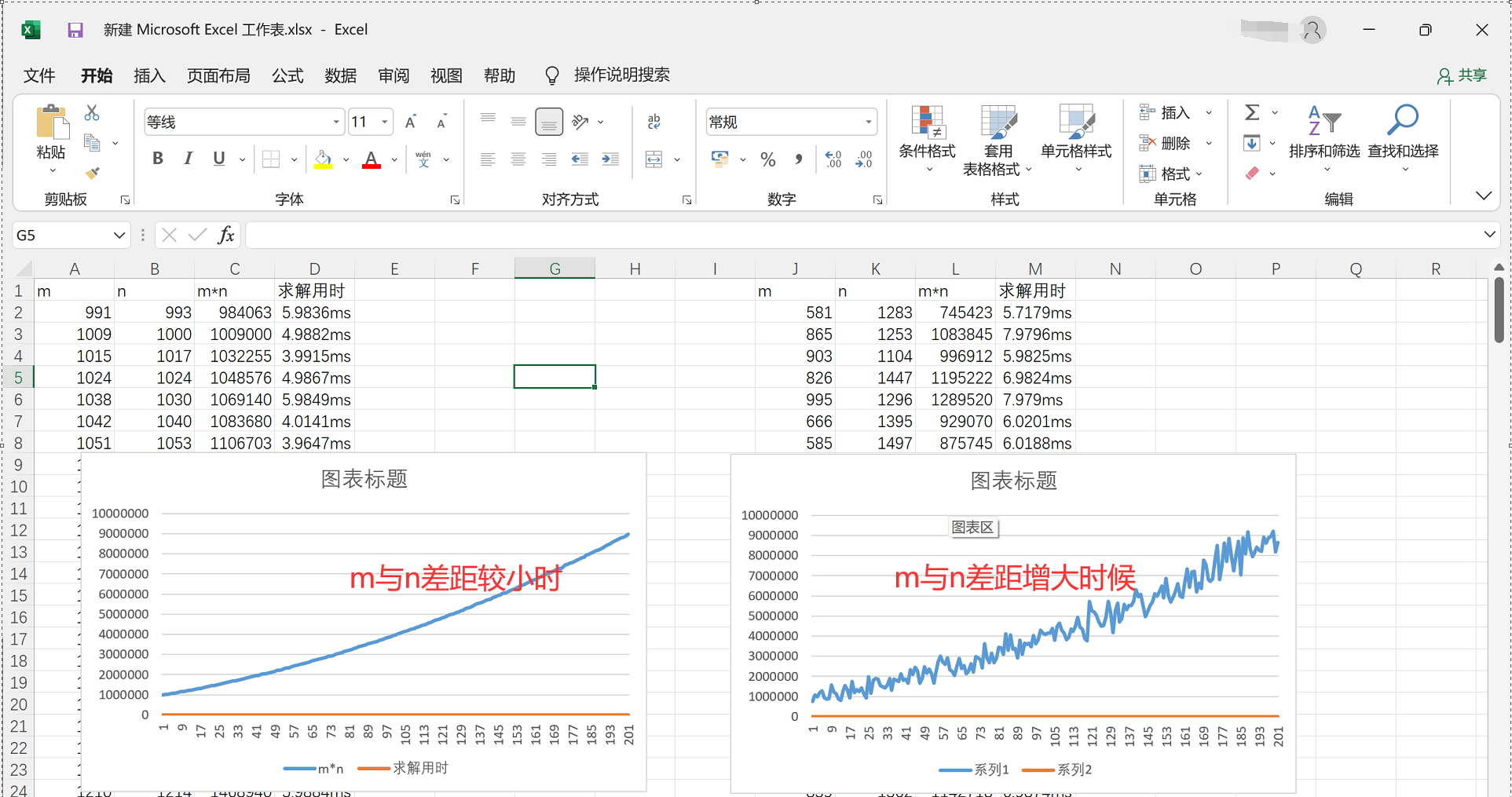
分析：根据本次实验得出的数据来看，两个字符串的长度m与n和求解用时之间没有什么规律。但从理论上讲，m*n越大，用时也应该越长

实验环境

goland

excel

疑难小结

​ 最开始根据m*n与求解用时的认为mn越大，求解用时越长，但是随之我增大m与n的之间的差距，在mn与求解用时的关系就出现了波动，说明nm和求解用时之间关联不是那么强烈，尤其是小数据范围内数据差距影响还是蛮大的，但是从理论上来讲mn越大，求解用时越长。

搜索算法应用(求解旅行商问题)

实验过程(请用简单的文字描述)

1. 首先对问题进行重述: 对旅行商问题使用回溯法进行分析

   问题：设有n个城市组成的交通图，一个售货员从住地城市出发，到其它城市各一次去推销货物，最后回到住地城市。假定任意两个城市i，j之间的距离dij(dij=dji)是已知的，问应该怎样选择一条最短的路线？

2. 确定实验算法思路:n 个城市组成的交通图中有 n 个节点，n 个节点之间的连 线的权值代表两个城市之间的距离，现在需要从一个点开始出发，假设这个开始 的点是 v0，需要到其他的所有点，在这个过程中需要找到最短的一个距离。搜 索整个解空间，当不满条件时，丢弃，继续搜索下一个儿子结点，如果所有儿子 结点都不满足，向上回溯到它的父节点。

3. 确定随机数范围：按照实际情况，旅行商问题使用回溯法进行计算的时候时 间复杂度应该是 O(n!)，这个时候应该呈现出爆炸式增长，那么 n 的区值就不能 是 500 这个样子的，这里从 15 开始计算，后来确定范围为[3，14]。

4. 实验过程大计划：使用golang进行编写，使用excel进行数据可视化

实验详细操作步骤或程序清单：

1. 造数据

   当我最开始进行生成数据的时候发现因为有随机数的存在，所以结果进行可视化 的时候效果不太好，后来对随机数的生成范围以及 n 的取值间隔进行了调整，发现随机数取值范围在[n,n+10] 的时候相较于我之前所造数据好很多。

2. 回溯法

   基本思想:

   在包含问题的所有解的解空间树中，按照深度优先搜索的策略，从根结点（开始结点）出发搜索解空间树

一个复杂问题的解决方案是由若干个小的决策步骤组成的决策序列，解决一个问题的所有可能的决策序列构成该问题的解空间

​ 求解过程:

• 用约束函数在扩展结点处剪除不满足约束的子树；
• 用限界函数剪去得不到问题解或最优解的子树。

1. 确定问题的解空间树，问题的解空间树应至少包含问题的一个（最优）解。

2. 确定结点的扩展规则。

3. 以深度优先方式搜索解空间树，并在搜索过程中可以采用剪枝函数来避免无效搜索。

   回溯法 = 深度优先搜索 + 剪枝

   搜索过程:

   扩展结点进行扩展的时候考虑约束条件和限界条件，如果说两个条件都满足 的话继续往下面进行搜索，如果到叶子结点的时候开始寻找最优解。 如果访问到 n 个节点,要判断是否形成回路，如果当前值优于最优值，更新最 优值和最优解。形成回路的条件就是 x[n-1]与 x[n]连通，x[n]与 x[1]连通，在形成 环路的时候，如果当前值优于最优值，更新最优值和最优解，best1=inf 说明还没 有广搜到一条回路，那就先试着求出一个可行解，接下来继续判断找到最优解， 并将最优解进行更新。 如果说当前在第 i 层，还得继续寻找。判断是否可以进入 x[j]子树，x[i-1]与 x[j]连通使得 1-i 层连成一条路径且累计花费优于目前最优值，可以进入 x[j]子树， 这里要做的就是交换 x[i]与 x[j],进入 i+1 层，思想类似于 n 的全排列问题，递归求 解，best1==inf 的时候就说明还没有通过广度优先搜索找到一条回路，那就先试 着求出一个可行解，现在的解就是 x[1],x[2]…x[i]…x[j]…x[n]，接下来判断是否满足 条件，如果说满足条件的话就进行交换，然后更新路径的长度进入第 i+1 层，在 回溯的时候需要还原路径的长度，然后重新交换 x[i]和 x[j]的位置进行还原。

   3.程序清单:

   回溯法：

   func BackTrack(t int) {
       if t > n {
           if g[x[n]][1] != -1 && (cl+g[x[n]][1] < bestl) { // 最后一个城市与出发的城市之间有路径 且当前总距离比当前最优值小
               for j := 0; j <= n; j++ {
                   bestx[j] = x[j] // 将当前路径的解 赋值给最优路径解
               }
               bestl = cl + g[x[n]][1] // 最优解为当进已走的长度 + 最后一个城市到 初始城市的距离 即: 回到初始城市
           }
       } else { // 没有到达叶子节点
           for j := t; j <= n; j++ { // 搜索所有与当前城市临近的剩余城市
               if g[x[t-1]][x[j]] != -1 && cl+g[x[t-1]][x[j]] < bestl {
                   // 如果第t-1个城市与第t个城市 有路径 且小于 best1
                   x[t], x[j] = x[j], x[t]   //交换t与j  即第t个要去的城市
                   cl = cl + g[x[t-1]][x[t]] // 路线长度增加
                   BackTrack(t + 1)          // 深度搜索下个节点
                   // 下个城市与当前城市 需要恢复 cl x[t]
                   cl = cl - g[x[t-1]][x[t]]
                   x[t], x[j] = x[j], x[t]
               }
           }
       }
   }

   总代码:

   package main
   
   import (
       "fmt"
       "math/rand"
       "time"
   )
   
   var (
       n     int             // 城市个数
       g     [][]int         // 存放城市之间距离
       cl    int     = 0     // 当前已走过的城市所用的路径长度
       bestl int     = 10000 // 表示当前找到的最短路径的路径长度
       x     []int           // 当前路线
       bestx []int           // 最优路线
   )
   
   func RandInt(min, max int) int { //生成随机数
       if min >= max || min == 0 || max == 0 {
           return max
       }
       return rand.Intn(max-min) + min
   }
   func main() {
       fmt.Println("n的大小\t运行时间\t最短路径长度")
       for n = 3; n < 17; n++ {
           // 初始化g 空间
           g = make([][]int, n+1)
           for i := 0; i < n+1; i++ {
               g[i] = make([]int, n+1)
           }
           for i := 1; i <= n; i++ {
               for j := 1; j <= n; j++ {
                   g[i][j] = RandInt(n, n+10)
                   //fmt.Scanf("%d", &g[i][j])
               }
           }
           x = make([]int, n+1)
           bestx = make([]int, n+1)
           // 初始化x   bestx
           for i := 1; i <= n; i++ {
               x[i] = i
               bestx[i] = 0
           }
           cl = 0
           bestl = 10000
           startTime := time.Now()
           BackTrack(2) // 第2个城市开始 默认第一个城市为出发点
           time.Sleep(1)
           sinceTime := time.Since(startTime)
           fmt.Println(n, "\t", int(sinceTime), "\t", bestl)
           //fmt.Println("最短路线长度:")
           //fmt.Println(bestl)
       }
       //fmt.Printf("请输入一共有几个城市:")
       //fmt.Scanln(&n)
       //fmt.Println("请输入城市之间的距离:")
       //// 初始化g 空间
       //g = make([][]int, n+1)
       //for i := 0; i < n+1; i++ {
       //    g[i] = make([]int, n+1)
       //}
       //for i := 1; i <= n; i++ {
       //    for j := 1; j <= n; j++ {
       //        fmt.Scanf("%d", &g[i][j])
       //    }
       //}
       // 初始化x[] int // 当前路线  //bestx[] int   // 最优路线 空间
       //x = make([]int, n+1)
       //bestx = make([]int, n+1)
       //// 初始化x   bestx
       //for i := 1; i <= n; i++ {
       //    x[i] = i
       //    bestx[i] = 0
       //}
       //BackTrack(2) // 第2个城市开始 默认第一个城市为出发点
       //fmt.Println("城市路线:")
       //for i := 1; i <= n; i++ {
       //    fmt.Printf("%d-", bestx[i])
       //}
       //fmt.Printf("%d", bestx[1])
       //fmt.Println("最短路线长度:")
       //fmt.Println(bestl)
   }
   
   func BackTrack(t int) {
       if t > n {
           if g[x[n]][1] != -1 && (cl+g[x[n]][1] < bestl) { // 最后一个城市与出发的城市之间有路径 且当前总距离比当前最优值小
               for j := 0; j <= n; j++ {
                   bestx[j] = x[j] // 将当前路径的解 赋值给最优路径解
               }
               bestl = cl + g[x[n]][1] // 最优解为当进已走的长度 + 最后一个城市到 初始城市的距离 即: 回到初始城市
           }
       } else { // 没有到达叶子节点
           for j := t; j <= n; j++ { // 搜索所有与当前城市临近的剩余城市
               if g[x[t-1]][x[j]] != -1 && cl+g[x[t-1]][x[j]] < bestl {
                   // 如果第t-1个城市与第t个城市 有路径 且小于 best1
                   x[t], x[j] = x[j], x[t]   //交换t与j  即第t个要去的城市
                   cl = cl + g[x[t-1]][x[t]] // 路线长度增加
                   BackTrack(t + 1)          // 深度搜索下个节点
                   // 下个城市与当前城市 需要恢复 cl x[t]
                   cl = cl - g[x[t-1]][x[t]]
                   x[t], x[j] = x[j], x[t]
               }
           }
       }
   }

   实验结果

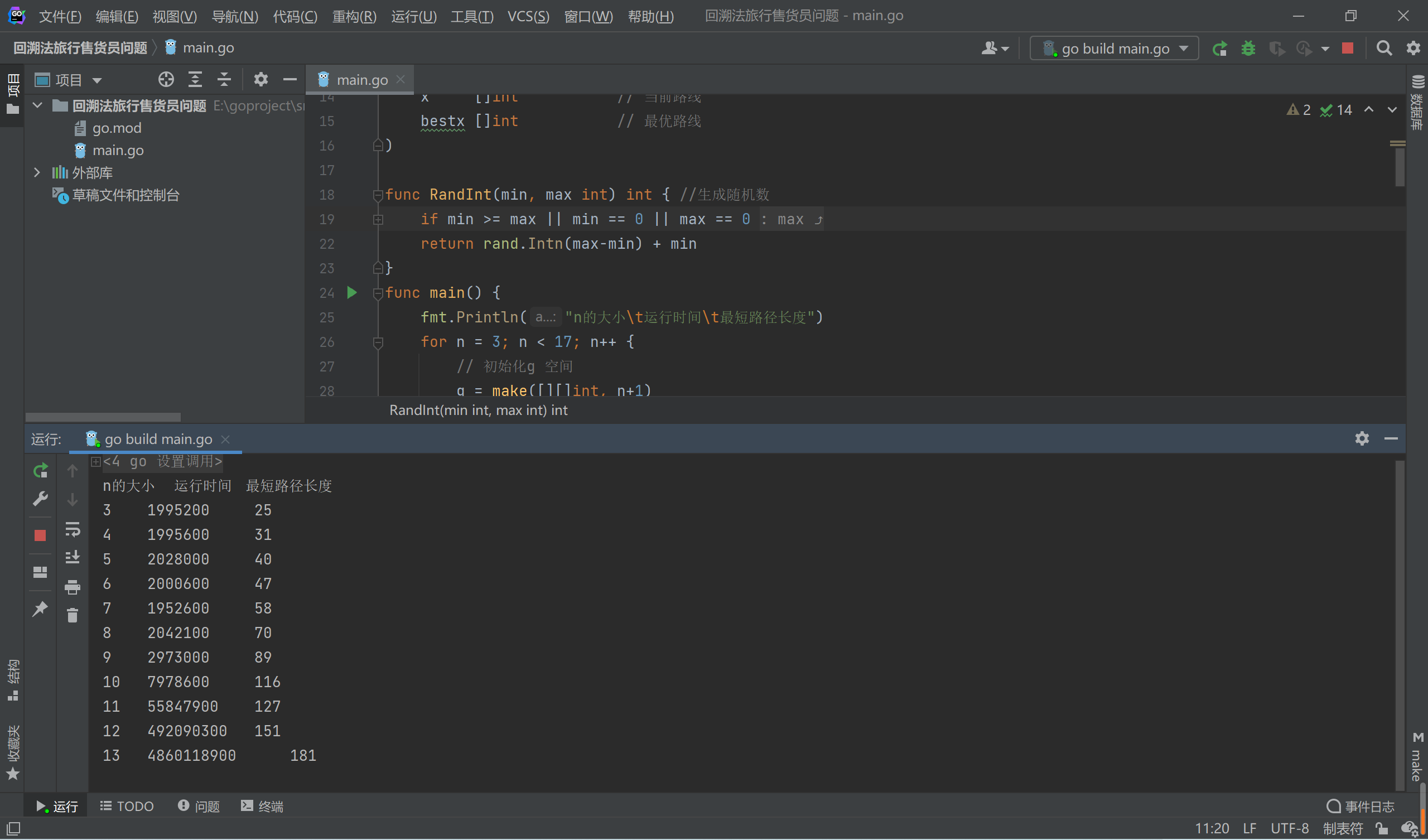
n的大小	运行时间	最短路径长度
3	1000700	25
4	1990500	31
5	1997300	40
6	1993900	47
7	1995100	58
8	2026400	70
9	1988900	89
10	7027000	116
11	48878500	127
12	505331800	151
13	4890401600	181
14	71729691200	207

数据可视化

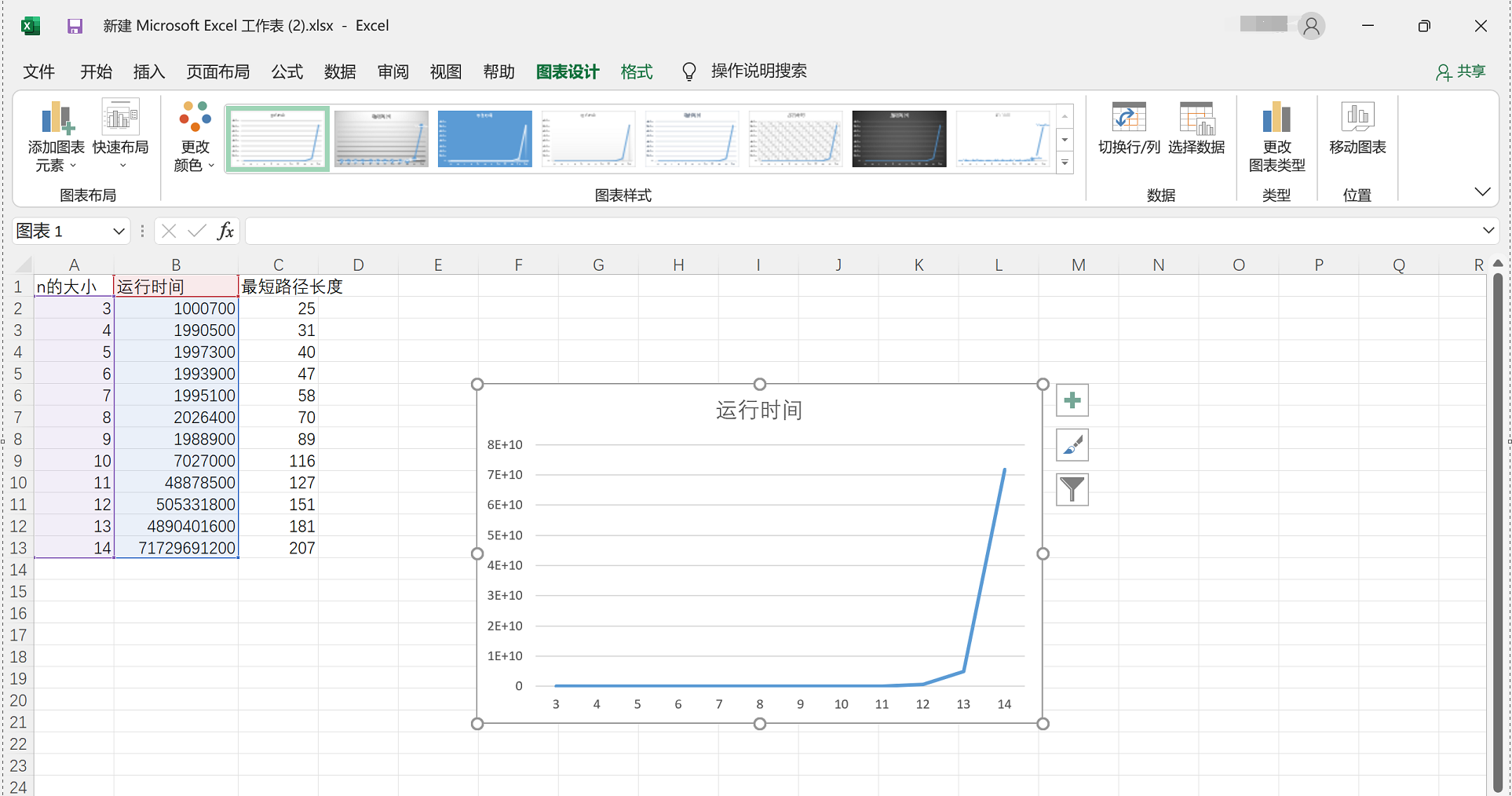
可以看到运行时间随着n呈现爆发式增长，与预期O(n!),发现和实际情况相符

实验环境

golang

excel

疑难小结

1.当n特别小时候运行时间特别块，计算时间需要提高精度

2.当n特别大的时候，需要很长时间才能跑出来，感觉减枝还有待优化

网络流算法应用(求网络的最大流)

实验过程(请用简单的文字描述)

1. 基本思想

​ 给定指定的一个有向图,其中有两个特殊的点源S(Sources)和汇T(Sinks),每条边有指定的容量(Capacity),求满足条件的从S到T的最大流(MaxFlow)。

2. 造数据，n∈[10,400]且 n%20==0 的顶点，随机生成完全图，通过计时求解n于时间关系，边数与时间的关系
3. 实验过程大计划 使用golang进行编写，使用excel做可视化分析

实验详细步骤或程序清单

1. 造数据

​ 随机数产出容量，采用完全图，初始流量设为0。

2. 求解过程

​ 采用深度优先遍历方法求从起点s到终点t的增广路径，顶点i的标记为(p[i],a[i])，p[i]表示顶点i在增广路径上的前驱顶点，如果为反向边，p[i]表示的前驱结点前加上一个负号。

3. 采用深度优先遍历方法求从起点s到终点t的增广路径，顶点i的标记为(p[i],a[i])，p[i]表示顶点i在增广路径上的前驱顶点，如果为反向边，p[i]表示的前驱结点前加上一个负号。

4. 程序清单

   求增广路径

   // 求增广路径路径
   func DFS(u int) { // 从顶点出发求一条增广路径
       if visited[t] == 1 {
           return
       }
       visited[u] = 1 //置已访问标志
       //lnng := visited
       //fmt.Println(lnng)
       //lnng2 := pre
       //fmt.Println(lnng2)
       for v := 1; v <= t; v++ { //遍历向前
           if c[u][v] > 0 && c[u][v] != INF && visited[v] == 0 && c[u][v] > f[u][v] {
               a[v] = c[u][v] - f[u][v]
               pre[v] = u //
               DFS(v)
           }
       }
       for v := 1; v <= t; v++ {
           if c[v][u] > 0 && c[v][u] != INF && visited[v] == 0 && f[v][u] > 0 {
               a[v] = f[v][u]
               pre[v] = -u
               DFS(v)
           }
       }
   }

   总代码

   package main
   
   import (
       "fmt"
       "math/rand"
       "time"
   )
   
   const (
       INF = 0xffffffff // 无限大的值
   )
   
   var (
       n, s, t int
       //n = 7                                         //  表示顶点个数
       //s = 0                                         //  表示起点
       //t = n - 1                                     //  表示终点
       //f = [7][7]int{{0, 6, 10, INF, INF, INF, INF}, // 一个网络流
      	//	{INF, 0, INF, 3, 6, INF, INF}, {INF, 3, 0, 0, INF, 7, INF},
      	//	{INF, INF, INF, 0, 1, 1, 3}, {INF, INF, INF, INF, 0, INF, 7},
      	//	{INF, INF, INF, 1, INF, 0, 6}, {INF, INF, INF, INF, INF, INF, 0}}
       //c = [7][7]int{{0, 8, 14, INF, INF, INF, INF}, //一个网络流容量
      	//	{INF, 0, INF, 3, 6, INF, INF}, {INF, 5, 0, 3, INF, 8, INF},
      	//	{INF, INF, INF, 0, 4, 3, 10}, {INF, INF, INF, INF, 0, INF, 7},
      	//	{INF, INF, INF, 3, INF, 0, 6}, {INF, INF, INF, INF, INF, INF, 0}}
       f    [][]int
       c    [][]int
       maxf = 0 // 最大流
   
       pre     []int
       a       []int //
       visited []int // 求解过程
   )
   
   func main() {
       fmt.Println("n\t边的个数\t运行时间")
       for n = 10; n < 400; n++ {
           if n%20 != 0 {
               continue
           }
           t = n - 1
           s = 0
           maxf = 0
           //初始化实际流量为0 残存流量
           f = make([][]int, n+1)
           for i := range f {
               f[i] = make([]int, n+1)
           }
           c = make([][]int, n+1)
           for i := range c {
               c[i] = make([]int, n+1)
           }
           //    先按完全图构建
           for i := 0; i < n; i++ {
               for j := 0; j < n; j++ {
                   if i < j {
                       c[i][j] = rand.Int() % 100
                   }
               }
           }
           for i := 1; i < n; i++ { // 起点没有进入边
               c[i][1] = 0
           }
           for i := 1; i <= n; i++ { // 终点没有出发点3
               c[n][i] = 0
           }
           timeStart := time.Now()
           FordFulkerson(n)
           spentTime := time.Since(timeStart)
           m := n * (n - 1) / 2
           fmt.Println(n, "\t", m, "\t", int(spentTime))
       }
   }
   func FordFulkerson(n int) {
       for {
           visited = make([]int, n+1)
           a = make([]int, n+1)
           pre = make([]int, n+1)
           for i := 0; i < n; i++ {
               pre[i] = i
           }
           //pre = [7]int{-1, -1, -1, -1, -1, -1, -1}
           pre[s] = 0
           a[s] = INF
           DFS(s)
           if visited[t] == 0 {
               break
           }
           //fmt.Println(pre)
           argument(pre)
           //fmt.Println()
       }
       for v := 1; v <= t; v++ {
           // 从起点流出的流量和为最大
           if c[s][v] != 0 && c[s][v] != INF {
               maxf = maxf + f[s][v]
           }
       }
       //fmt.Println(f)
       //fmt.Println("网络最大流为:", maxf)
   }
   func DFS(u int) { // 从顶点出发求一条增广路径
       if visited[t] == 1 {
           return
       }
       visited[u] = 1 //置已访问标志
       //lnng := visited
       //fmt.Println(lnng)
       //lnng2 := pre
       //fmt.Println(lnng2)
       for v := 1; v <= t; v++ { //遍历向前
           if c[u][v] > 0 && c[u][v] != INF && visited[v] == 0 && c[u][v] > f[u][v] {
               a[v] = c[u][v] - f[u][v]
               pre[v] = u //
               DFS(v)
           }
       }
       for v := 1; v <= t; v++ {
           if c[v][u] > 0 && c[v][u] != INF && visited[v] == 0 && f[v][u] > 0 {
               a[v] = f[v][u]
               pre[v] = -u
               DFS(v)
           }
       }
   }
   
   func argument(pre []int) {
       //fmt.Println(pre)
       //fmt.Println(a)
       var min = INF
       for v := s; v <= t; v++ {
           if a[v] != 0 && a[v] < min {
               min = a[v] //求最小流
           }
       }
       var u = t
       v := pre[u] // 从路径的终点开始调整
       for {
           if v >= 0 { // 向前调整
               f[v][u] = f[v][u] + min
               u = v
           } else {
               f[u][-v] = f[u][-v] - min // 向后调整
               u = -v
           }
           if u == s {
               break
           }
           //fmt.Println(u)
           v = pre[u]
       }
   }

实验结果

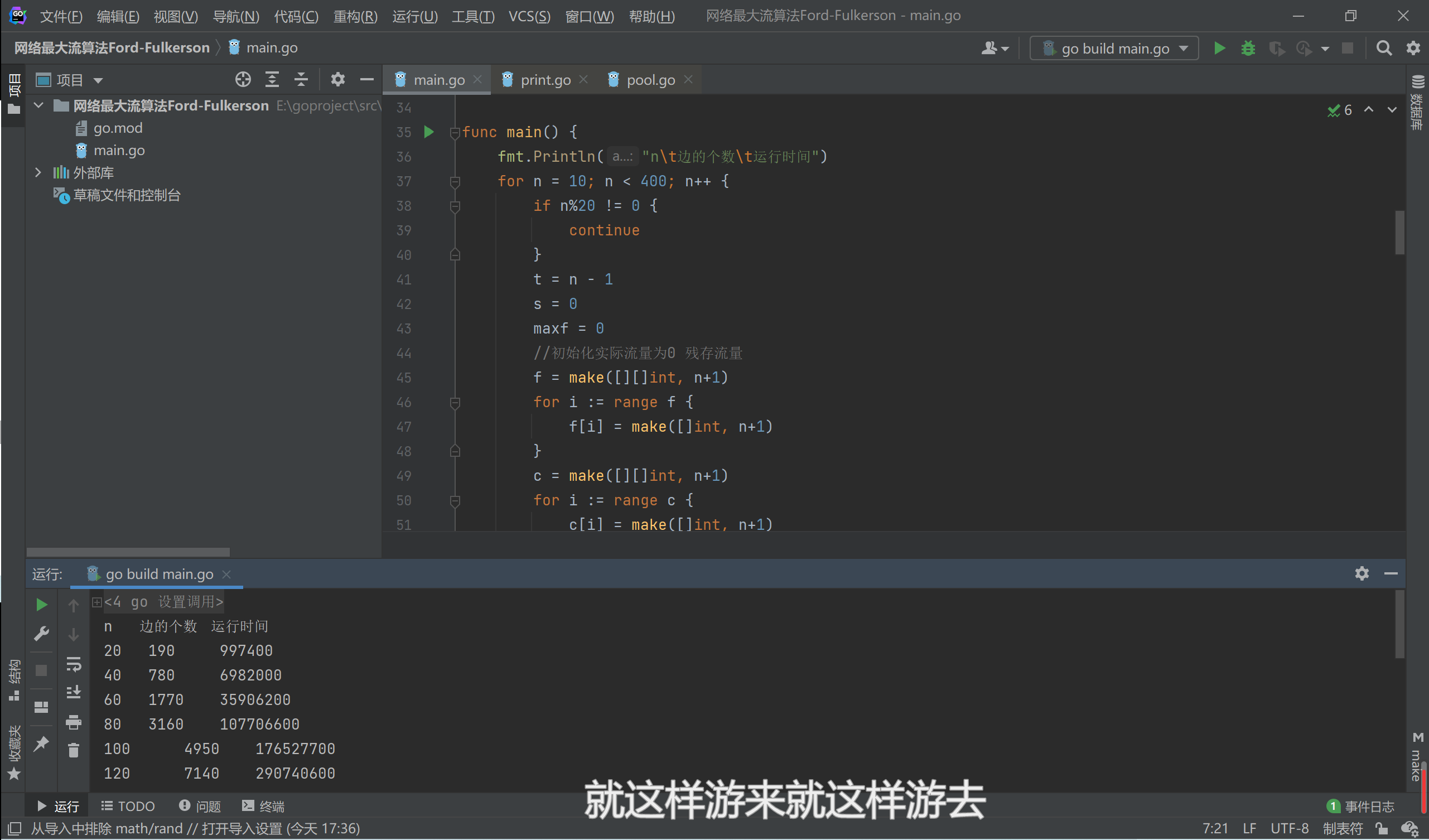
n	边的个数	运行时间
20	190	997400
40	780	6982000
60	1770	35906200
80	3160	1.08E+08
100	4950	1.77E+08
120	7140	2.91E+08
140	9730	4.74E+08
160	12720	7.24E+08
180	16110	1.16E+09
200	19900	1.47E+09
220	24090	1.97E+09
240	28680	2.87E+09
260	33670	3.44E+09
280	39060	4.03E+09
300	44850	6.07E+09
320	51040	7.38E+09
340	57630	1.19E+10
360	64620	1.08E+10
380	72010	1.21E+10

数据可视化

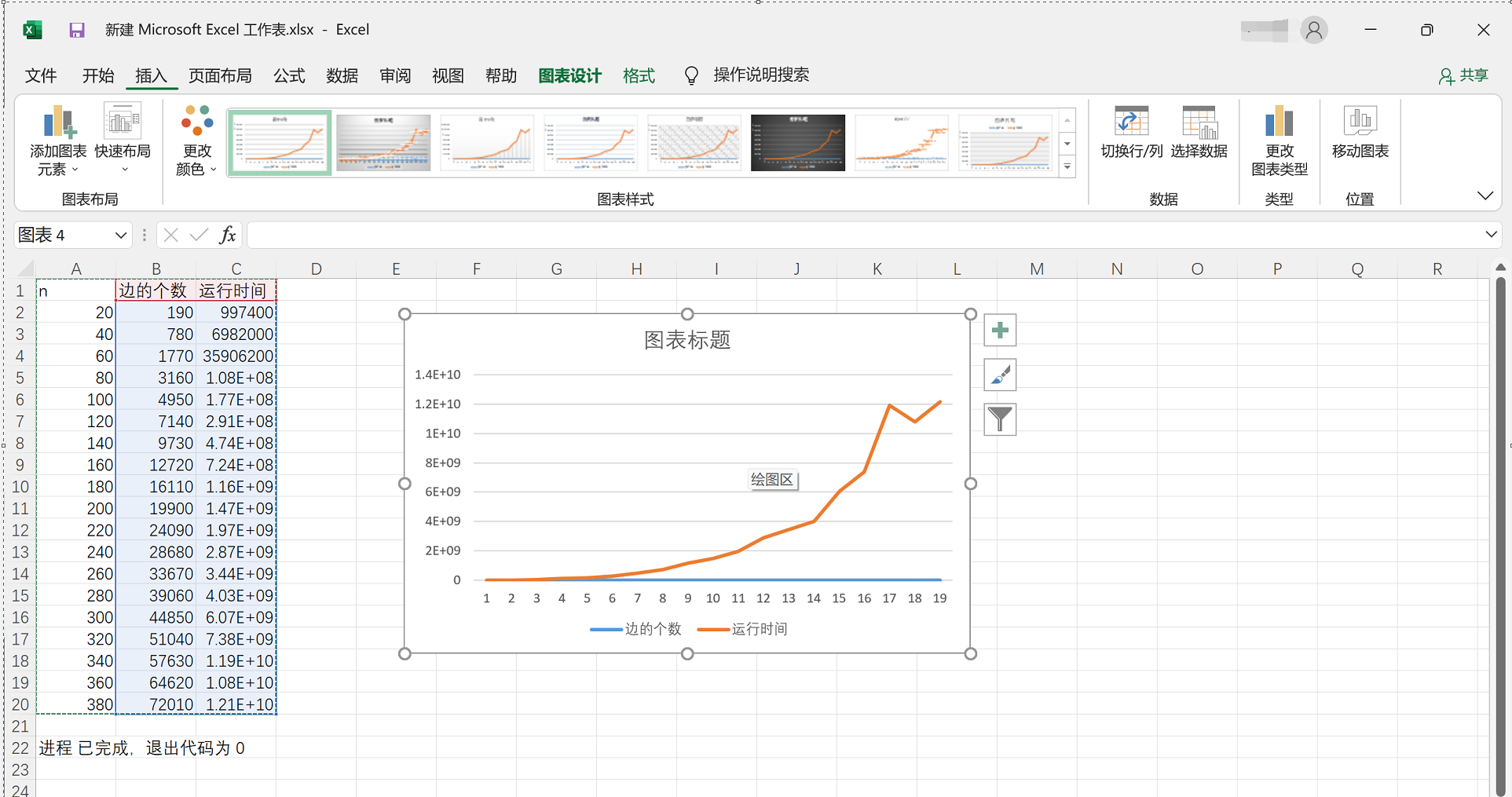
分析:

​ 若网络G中有n个顶点和e条边，FordFulkerson()算法中，找一条增广路径的时间为O(e)，调整流量的时间为O(e)，设f表示算法找到的最大流，迭代次数最多为|f|，所以该算法的时间复杂度为O(e|f*|)

实验环境

excel

golang

疑难小结

1. 由于生成的是完全图，在判断边的个数和运算时间的关系感觉还具有偏向性质，这样边数就和顶点有着某种关系，感觉还能优化一下造的数据
2. 这样求增广路径还有概率重复操作，可以优化一下广度优先

   随机化算法应用(用随机算法计算椭圆面积)

   1.实验过程(请用简单的文字描述)

1.首先对问题进行重述使用随机算法计算椭圆面积，获得精度比较高结果，并输出；

2.构建椭圆

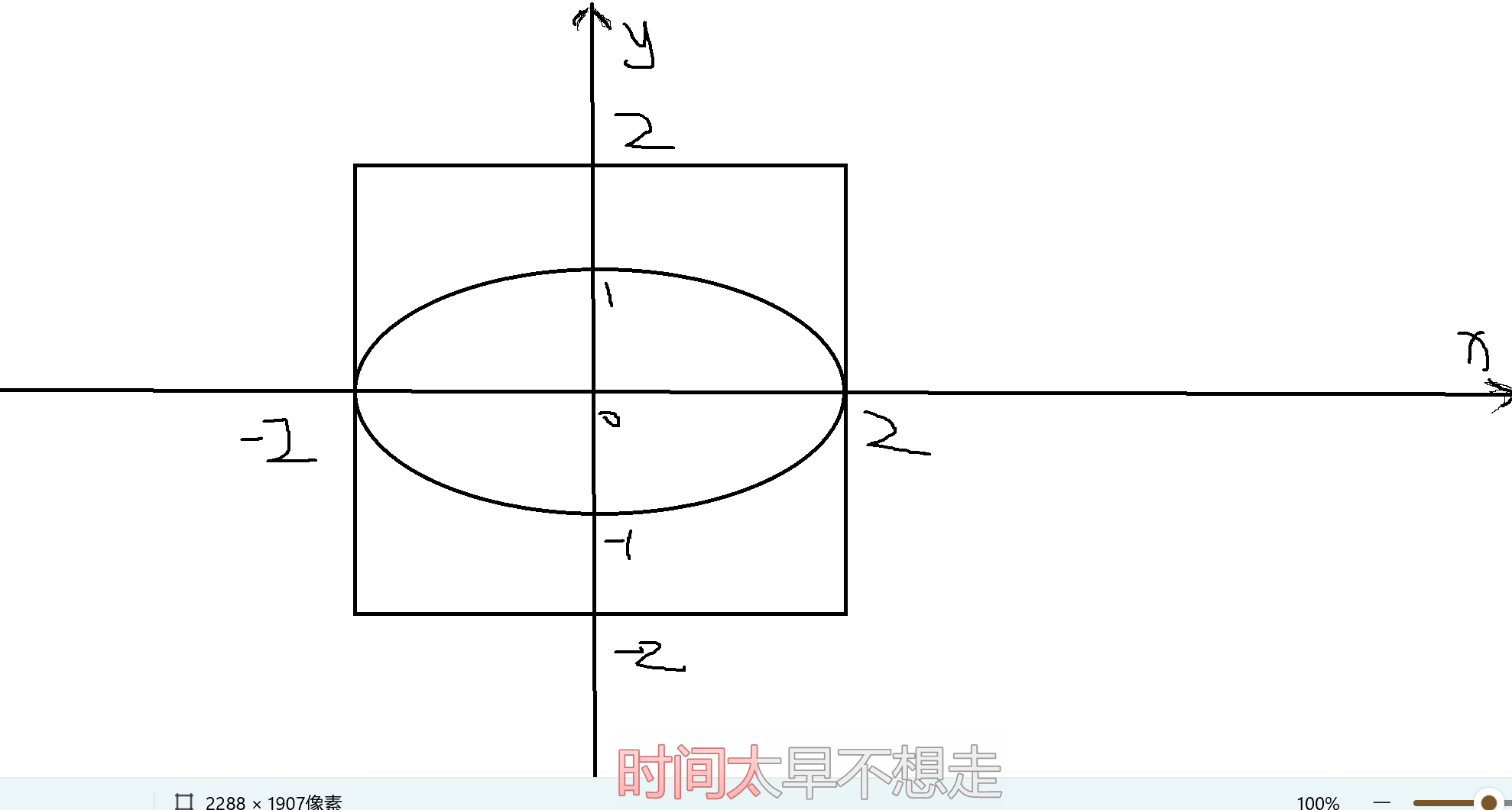
所以面积等于:2×1×Π

3.确定随机数范围，因为n过小时波动太大，所以n 100000开始

每次递增100000，来使数据不那么波动

通过面积比来确定椭圆面积，即随机点落在椭圆内比落在正方体内

4.实验过程大计划:使用golang进行编写，使用excel进行数据可视化

实验详细操作步骤或程序清单

1. 使用随机数生成0~2的随机数，因为对称在四个象限的所占比例一样，所以只需要算一个象限就行了
2. 截取小数位数来确定相同的位数

程序清单

梯度化取n

//梯度化取n
if n < 1000{
            if n%50 != 0{
                continue
            }
        }else if n < 100000{
            if n %1000 != 0{
                continue
            }
        }else if n < 100000000{
            if n % 100000 != 0{
                continue
            }
        }

随机化点

    x := RandFloat64(0.000000000001,2.000000000000)
    y := RandFloat64(0.000000000001,2.000000000000)

总代码

package main

import (
    "fmt"
    "math"
    "math/rand"
    "strconv"
    "strings"
    "time"
)
func RandFloat64(min, max float64) float64 {
    if min >= max || min == 0 || max == 0 {
        return max
    }
    minStr := strconv.FormatFloat(min, 'f', -1, 64)
    // 不包含小数点
    if strings.Index(minStr, ".") == -1 {
        return max
    }
    multipleNum := len(minStr) - (strings.Index(minStr, ".") + 1)
    multiple := math.Pow10(multipleNum)
    minMult := min * multiple
    maxMult := max * multiple
    randVal := RandInt64(int64(minMult), int64(maxMult))
    result := float64(randVal) / multiple
    return result
}
//随机整数
func RandInt64(min, max int64) int64 {
    if min >= max || min == 0 || max == 0 {
        return max
    }
    return rand.Int63n(max - min + 1) + min
}
func FloatRound(f float64, n int) float64 {
    n10 := math.Pow10(n)
    return math.Trunc((f)*n10)/n10
}
func main()  {
    //随机点范围0~2
    fmt.Println("n\t面积\t正确位数\t运行时间")
    for n := 1; n <= 100000000; n++ {
        if n < 1000{
            if n%50 != 0{
                continue
            }
        }else if n < 100000{
            if n %1000 != 0{
                continue
            }
        }else if n < 100000000{
            if n % 100000 != 0{
                continue
            }
        }
        area := n
        inEllipse := 0
        start := time.Now()
        for n != 0{
            n = n - 1
            x := RandFloat64(0.000000000001,2.000000000000)
            y := RandFloat64(0.000000000001,2.000000000000)
            lnng := x*x/4+y*y
            if lnng <= 1{
                inEllipse = inEllipse + 1
            }
        }
        n =area
        //fmt.Println(area)
        inEllipseFloat := float64(inEllipse)
        areaFloat := float64(area)
        results := inEllipseFloat/areaFloat*16
        sincereTime := time.Since(start)
        //fmt.Println(results)
        //fmt.Printf("%d %.8f\n",area,results)

        //subtraction := results -  6.28
        //6.2831852
        lnng := 2*1*math.Pi
        //lnng = FloatRound(lnng,1)
        //results = FloatRound(results,1)
        //fmt.Println(lnng," ",results)
        //fmt.Println(results)
        //fmt.Println(FloatRound(lnng,4))
        //fmt.Println(results,FloatRound(results,2),FloatRound(lnng,2))
        for i := 7; i >= 0; i-- {

            if FloatRound(lnng,i) == FloatRound(results,i){
                fmt.Println(n,"\t",results,"\t",i,"\t",int(sincereTime))
                break
            }
        }
    }
}

实验结果

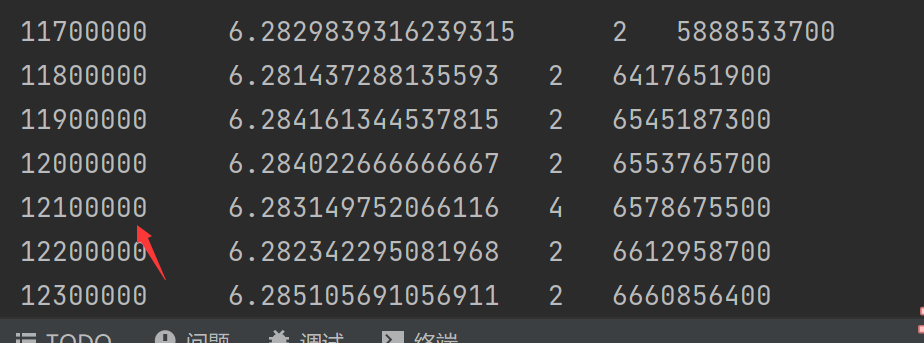
n	面积	正确位数	运行时间
50	6.4	0	0
100	6.88	0	0
250	6.272	1	0
300	6.88	0	0
550	6.138182	0	0
600	6.373333	0	0
650	6.449231	0	997800
700	6.217143	1	0
800	6.34	0	997300
850	6.456471	0	0
950	6.349474	0	996800
1000	6.256	1	0
2000	6.552	0	997100
3000	6.224	1	998500
4000	6.508	0	1993800
5000	6.3712	0	1994100
6000	6.256	1	2992000
7000	6.315429	0	2992500
8000	6.196	0	3990000
9000	6.108444	0	2991900
10000	6.2288	1	3989600
11000	6.270545	1	3989100
12000	6.292	1	4985300
13000	6.359385	0	4986700
14000	6.288	2	4986900
15000	6.270933	1	7016700
16000	6.426	0	5950000
17000	6.369882	0	6982400
18000	6.276444	1	7977500
19000	6.459789	0	6984500
20000	6.228	1	7975600
21000	6.221714	1	9792800
22000	6.188364	0	8976300
23000	6.247652	1	8975500
24000	6.226	1	8976800
25000	6.30336	0	10970300
26000	6.332308	0	9973700
27000	6.275556	1	9972600
28000	6.296571	1	11968300
29000	6.340966	0	11968400
30000	6.304	0	11966500
31000	6.352516	0	12965300
32000	6.264	1	12967100
33000	6.260848	1	13962000
34000	6.296	1	13964300
35000	6.2656	1	13960800
36000	6.259556	1	14992600
37000	6.279351	1	16921400
38000	6.262737	1	16960800
39000	6.232205	1	15956200
40000	6.3076	0	19944800
41000	6.295415	1	17951100
42000	6.316571	0	18948400
43000	6.313674	0	18949300
44000	6.258909	1	17951800
45000	6.249956	1	18951100
46000	6.269217	1	20941700
47000	6.267234	1	19947000
48000	6.312	0	21943000
49000	6.282776	2	20942500
50000	6.29728	1	21940500
51000	6.274824	1	21954800
52000	6.281846	2	22958100
53000	6.270491	1	21911000
54000	6.279407	1	21971600
55000	6.243782	1	22941700
56000	6.261143	1	23936600
57000	6.23607	1	22934700
58000	6.273931	1	25342000
59000	6.244068	1	25899500
60000	6.274667	1	24965700
61000	6.19541	0	23935600
62000	6.242065	1	24899500
63000	6.280381	2	24961200
64000	6.34275	0	26909000
65000	6.268554	1	24960000
66000	6.307636	0	26923500
67000	6.275821	1	25901600
68000	6.314824	0	25931000
69000	6.337623	0	26957900
70000	6.252343	1	27897000
71000	6.276958	1	27953900
72000	6.276444	1	27895200
73000	6.289753	2	27923000
74000	6.274811	1	29954800
75000	6.26816	1	28889800
76000	6.283158	4	29919900
77000	6.300675	0	28922200
78000	6.325949	0	28953600
79000	6.326684	0	28926200
80000	6.2772	1	31910500
81000	6.289185	2	31886700
82000	6.291317	1	30940500
83000	6.272	1	34916200
84000	6.29619	1	35904700
85000	6.275576	1	34905800
86000	6.284465	2	34940100
87000	6.304	0	34900400
88000	6.235455	1	36157400
89000	6.254742	1	37901400
90000	6.314844	0	47873500
91000	6.317714	0	36409400
92000	6.280174	2	36934400
93000	6.273548	1	37866200
94000	6.278298	1	38452500
95000	6.273684	1	36894500
96000	6.301167	0	37909000
97000	6.298887	1	37891200
98000	6.268735	1	38900400
99000	6.286061	2	38865400
100000	6.25328	1	40888900
200000	6.29984	1	75827400
300000	6.284587	2	1.14E+08
400000	6.29292	1	1.52E+08
500000	6.297632	1	1.9E+08
600000	6.300133	0	2.33E+08
700000	6.289097	2	2.63E+08
800000	6.28908	2	2.96E+08
900000	6.286222	2	3.38E+08
1000000	6.299024	1	3.9E+08
1100000	6.280873	2	4.07E+08
1200000	6.27564	1	4.71E+08
1300000	6.283545	3	5.25E+08
1400000	6.288446	2	6.91E+08
1500000	6.280661	2	6.46E+08
1600000	6.28694	2	6.65E+08
1700000	6.282776	2	6.6E+08
1800000	6.287796	2	7.18E+08
1900000	6.282063	2	7.97E+08
2000000	6.278072	1	9.46E+08
2100000	6.283208	3	1.23E+09
2200000	6.280022	2	1.17E+09
2300000	6.272459	1	1.3E+09
2400000	6.283827	3	1.23E+09
2500000	6.287731	2	1.24E+09
2600000	6.283582	3	1.39E+09
2700000	6.282394	2	1.31E+09
2800000	6.282903	2	1.23E+09
2900000	6.281754	2	1.36E+09
3000000	6.281253	2	1.49E+09
3100000	6.279819	1	1.3E+09
3200000	6.29046	1	1.37E+09
3300000	6.286676	2	1.52E+09
3400000	6.284696	2	1.62E+09
3500000	6.288009	2	1.44E+09
3600000	6.284267	2	1.46E+09
3700000	6.281764	2	1.59E+09
3800000	6.279811	1	1.58E+09
3900000	6.285087	2	1.59E+09
4000000	6.28536	2	1.67E+09
4100000	6.290115	1	1.73E+09
4200000	6.284518	2	1.73E+09
4300000	6.283877	3	1.76E+09
4400000	6.282829	2	1.97E+09
4500000	6.286908	2	1.91E+09
4600000	6.282063	2	1.92E+09
4700000	6.283149	4	1.91E+09
4800000	6.278213	1	1.93E+09
4900000	6.283096	3	1.98E+09
5000000	6.285933	2	2.04E+09
5100000	6.277989	1	2.06E+09
5200000	6.285711	2	2.13E+09
5300000	6.28368	3	2.13E+09
5400000	6.286107	2	2.17E+09
5500000	6.282435	2	2.26E+09
5600000	6.279869	1	2.25E+09
5700000	6.280334	2	2.33E+09
5800000	6.281887	2	2.32E+09
5900000	6.281622	2	2.4E+09
6000000	6.28064	2	2.41E+09
6100000	6.282083	2	2.46E+09
6200000	6.28328	3	2.55E+09
6300000	6.28864	2	2.52E+09
6400000	6.284665	2	2.61E+09
6500000	6.277135	1	2.63E+09
6600000	6.279663	1	2.69E+09
6700000	6.28278	2	2.7E+09
6800000	6.284525	2	2.8E+09
6900000	6.28151	2	2.79E+09
7000000	6.280459	2	2.88E+09
7100000	6.281161	2	2.86E+09
7200000	6.286244	2	2.93E+09
7300000	6.281981	2	2.96E+09
7400000	6.285689	2	2.95E+09
7500000	6.283667	3	3.02E+09
7600000	6.290509	1	3.06E+09
7700000	6.276852	1	3.11E+09
7800000	6.285124	2	3.15E+09
7900000	6.280028	2	3.44E+09
8000000	6.28374	3	3.41E+09
8100000	6.288535	2	3.43E+09
8200000	6.287434	2	3.65E+09
8300000	6.282903	2	3.65E+09
8400000	6.283857	3	3.86E+09
8500000	6.28032	2	3.69E+09
8600000	6.287222	2	3.8E+09
8700000	6.283474	3	3.71E+09
8800000	6.279855	1	3.96E+09
8900000	6.278342	1	4.07E+09
9000000	6.283404	3	3.74E+09
9100000	6.282576	2	3.85E+09
9200000	6.27935	1	4.51E+09
9300000	6.281237	2	3.94E+09
9400000	6.279619	1	3.98E+09
9500000	6.279828	1	4.45E+09
9600000	6.286072	2	4.06E+09
9700000	6.286959	2	4.43E+09
9800000	6.282785	2	3.97E+09
9900000	6.28725	2	4.05E+09
10000000	6.282206	2	4.46E+09
10100000	6.285659	2	4.27E+09
10200000	6.278947	1	4.76E+09
10300000	6.277605	1	5E+09
10400000	6.287028	2	4.82E+09
10500000	6.283712	3	4.85E+09
10600000	6.281265	2	5.81E+09
10700000	6.27959	1	5.49E+09
10800000	6.281514	2	4.95E+09

数据可视化

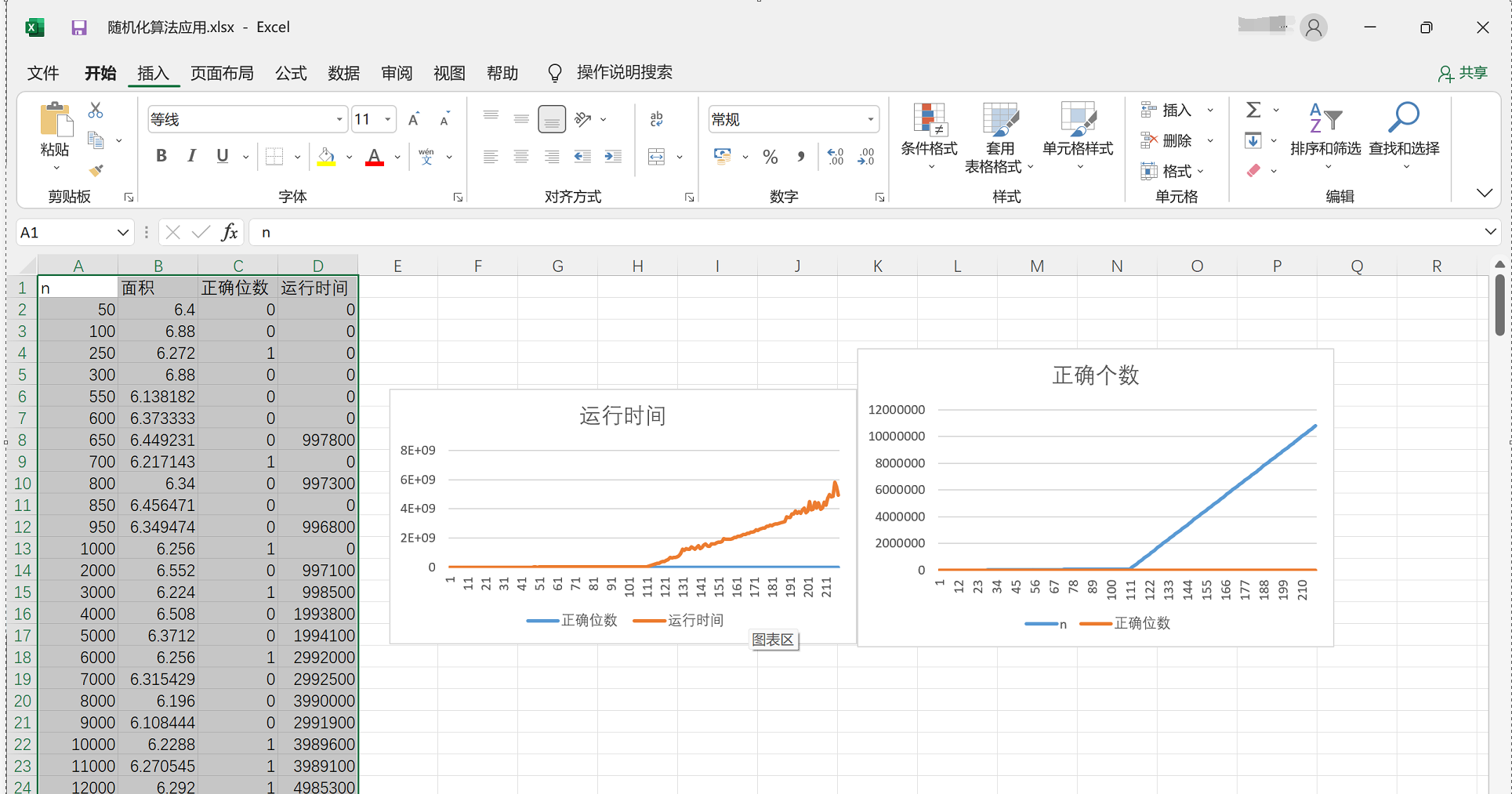
可以发现随着n的增大，数据的相当位数越多，数据越平稳，同样的运行时间更长，符合预期

实验环境

golang

excel

疑难小结

当n逐渐增大时数据的精确度很难提高了，运行了一会最多相当的位数也就是4，后来很蛮了 ，随着位数的增大，数据精度也需要提高了，即生成的随机坐标的精度，推论出坐标精度决定数据的精度